概述
本文将带领读者从零实现 Uniswap V3 的所有功能。在内容上,本文主要参考了 Constructor | Uniswap V3 Core Contract Explained 系列教程,同时部分内容也来自 Uniswap V3 Development Book 以及 Paco 博客。
本文内的代码可以参考 clamm 代码库。
构造器与初始化
初始化项目。我们首先一个文件夹用于存储 Uniswap V3 和我们自己的代码:
mkdir uniswap & cd uniswap
git clone https://github.com/Uniswap/v3-core.git
mkdir clamm & cd clamm
forge init --vscode
最后,我们可以获得以下文件目录格式:
.
├── clamm
│ ├── README.md
│ ├── foundry.toml
│ ├── lib
│ ├── remappings.txt
│ ├── script
│ ├── src
│ └── test
└── v3-core
├── LICENSE
├── README.md
├── audits
├── bug-bounty.md
├── contracts
├── echidna.config.yml
├── hardhat.config.ts
├── package.json
├── test
├── tsconfig.json
└── yarn.lock
接下来,我们可以在 clamm 的 src 文件夹内创建 CLAMM.sol 文件,我们将在该文件内编写 Uniswap V3 Pool 合约。注意,在本文内,我们目前不会构造 Factroy 合约,所以我们需要将 Uniswap V3 的原版合约修改为构造器初始化版本。
// SPDX-License-Identifier: GPL-2.0-or-later
pragma solidity ^0.8.20;
contract CLAMM {
address public immutable token0;
address public immutable token1;
uint24 public immutable fee;
int24 public immutable tickSpacing;
uint128 public immutable maxLiquidityPerTick;
constructor (address _token0, address _token1, uint24 _fee, int24 _tickSpacing) {
token0 = _token0;
token1 = _token1;
fee = _fee;
tickSpacing = _tickSpacing;
maxLiquidityPerTick = Tick.tickSpacingToMaxLiquidityPerTick(_tickSpacing);
}
}
在此处,我们使用了 Tick 库中的 tickSpacingToMaxLiquidityPerTick 函数。为了方便读者理解,我们首先介绍 Tick 的概念。众所周知,在 Uniswap V3 内部,存在价格区间概念,我们使用 Tick 标记价格区间的上限和下限。
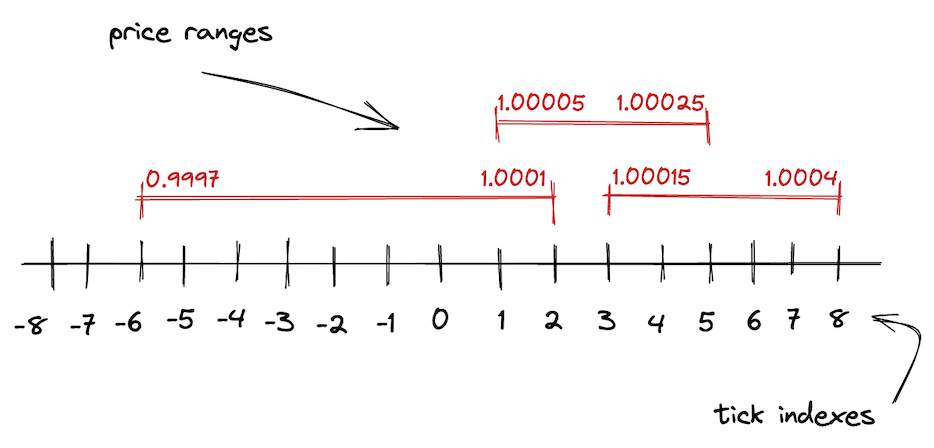
在 Uniswap V3 内,我们使用 $p(i) = 1.0001^i$ 来计算第 i 个 Tick 对应的具体价格。在上文的代码内出现了 _tickSpacing 的概念。这是指在 Uniswap V3 内,我们不会使用 0, 1, 2 这种索引,在大部分情况下,我们都是使用的类似 0, 10, 20 这种更大区间的索引,而 _tickSpacing 则代表价格区间的长度。比如在 _tickSpacing = 10 的情况下,0, 10, 20, 30 等数值就是有效 Tick,而 11 等就是无效的索引。大区间意味着更少的价格区间,但也意味着更低的价格精度。相反的,小区间意味着更高的价格精度,但也会带来更高的 gas 消耗,我们会在后文介绍其中的原因。Uniswap 允许使用 10、60 或 200 作为 _tickSpacing 的参数。
当我们了解了 _tickSpacing 的概念后,我们就可以理解 tickSpacingToMaxLiquidityPerTick 方法的含义。其功能在于计算每一个有效 Tick 下可允许的最大流动性。当使用小区间时,单个区间内的最大流动性会较低,反之则较高。我们可以在 clamm/src/libraries/Tick.sol 内编写 tickSpacingToMaxLiquidityPerTick 函数。
// SPDX-License-Identifier: GPL-2.0-or-later
pragma solidity ^0.8.20;
import "./TickMath.sol";
library Tick {
function tickSpacingToMaxLiquidityPerTick(int24 tickSpacing) internal pure returns (uint128) {
int24 minTick = (TickMath.MIN_TICK / tickSpacing) * tickSpacing;
int24 maxTick = (TickMath.MAX_TICK / tickSpacing) * tickSpacing;
uint24 numTicks = uint24((maxTick - minTick) / tickSpacing) + 1;
return type(uint128).max / numTicks;
}
}
此处使用 TickMath.sol 是一个用于 Tick 相关计算的数学库,读者可以直接在 v3-core/contracts/libraries/TickMath.sol 内复制。我们不会在本文介绍该数学库的具体原理,未来会有单独的博客介绍。
此处的 MIN_TICK 和 MIN_TICK 就是在 tickSpacing = 1 的情况下,最大的索引值和最小的索引值。我们第一步使用 (TickMath.MIN_TICK / tickSpacing) * tickSpacing; 计算出在当前 tickSpacing 下的最小索引值。我们可以使用 chisel 工具看看上述代码的作用。
➜ int24 internal constant MIN_TICK = -887272;
➜ int24 tickSpacing = 10;
➜ int24 minTick = (MIN_TICK / tickSpacing) * tickSpacing;
➜ minTick
Type: int24
├ Hex: 0xf2761a
├ Hex (full word): 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffffff2761a
└ Decimal: -887270
可以看到 (TickMath.MIN_TICK / tickSpacing) * tickSpacing; 就是将原本的 MIN_TICK 修正为 tickSpacing 的倍数。根据我们上文的讨论,所有不是 tickSpacing 倍数的索引实际上都是无效的。简单来说,计算 minTick 和 maxTick 就是计算在当前 tickSpacing 下最大和最小的有效索引值。接下来,我们需要计算当前 tickSpcing 下有效 Tick 的数量。注意此处我们计算的是 有效 Tick 的数量而不是区间的数量,所以我们需要对 max - min / tickSpcing 计算出的区间数量增加 1 以计算 Tick 数量,即 uint24((maxTick - minTick) / tickSpacing) + 1 。最后,Uniswap 使用 uint128 存储流动性数量,所以此处只需要 type(uint128).max / numTicks; 就可以计算出每一个有效 Tick 对应的流动性数量。
在
TickMath.sol的getSqrtRatioAtTick函数内,如果读者使用较新版本的 solidity 编译器,那么读者需要将require(absTick <= uint256(MAX_TICK), 'T');修改为require(absTick <= uint256(int256(MAX_TICK)), 'T');。
接下来,我们介绍 initialize 函数,initialize 函数用于初始化 Slot0 状态变量。众所周知,在 Solidity 内部,一个结构体内部所有元素如果长度累加到一起小于 256 bit ,那么将该结构体内的元素打包放在同一个存储槽内部。如果读者对存储部分不是特别熟悉,可以阅读 Solidity Gas 优化清单及其原理:存储、内存与操作符。而 Slot0 就是一个这样的结构体。该结构体占据了第一个存储槽。本文目前使用了一个 Slot0 的简化版本:
Slot0 public slot0;
struct Slot0 {
uint160 sqrtPriceX96;
int24 tick;
bool unlocked;
}
上述结构体内部 sqrtPriceX96 代表当前的方价格的开方,tick 则代表当前价格所位于的有效 Tick 数值,而 unlocked 则用于防止重入攻击。此处读者大概率好奇为啥使用价格的开方,这是因为 Uniswap 特殊的数学。假设 token0 的数量为 $x$,而 token1 的数量为 $y$。在 Uniswap V3 内,我们定义:
$$
L = \sqrt{xy} \\
\sqrt{P} = \sqrt{\frac{y}{x}}
$$
关于为什么 Uniswap V3 使用了 $\sqrt{P}$ 变量,读者可以在后文的编码实践中体验到,或者去阅读 Uniswap V3 Development Book 中的数学推导部分。众所周知,Solidity 内不能存储浮点数,所以 Uniswap V3 使用了 $\sqrt{P} * 2^{96}$ 的方案来存储浮点数。正如上文所述,sqrtPriceX96 代表的价格与 Tick 是有关的,我们需要一个数学公式来转化:
$$
P = \left(\frac{\text{sqrtPriceX96}}{2^{96}}\right)^2 = {1.0001}^{\text{tick}} \\
2\log\left(\frac{\text{sqrtPriceX96}}{2^{96}}\right) = \text{tick}\log{1.0001} \\
\text{tick} = \frac{2\log\left(\frac{\text{sqrtPriceX96}}{2^{96}}\right)}{\log{1.0001}}
$$
在 TickMath 内已经包含了上述 sqrtPriceX96 与 tick 的转换计算函数,该函数被命名为 getTickAtSqrtRatio 函数。当我们具有以上知识后,我们就可以编写如下初始化函数:
function initialize(uint160 sqrtPriceX96) external {
require(slot0.sqrtPriceX96 == 0, 'Already initialized');
int24 tick = TickMath.getTickAtSqrtRatio(sqrtPriceX96);
slot0 = Slot0({
sqrtPriceX96: sqrtPriceX96,
tick: tick,
unlocked: true
});
}
流动性提供
mint 函数用于向流动性池内增加流动性。在本节中,我们将介绍 mint 函数的构成及相关数学计算与代码。另外,为了简化文章内容,我们并不会在本文内涉及手续费和预言机逻辑,同时我们也去掉了 mint 函数内的回调函数。所以,我们可以得到以下 mint 函数的定义:
function mint(
address recipient,
int24 tickLower,
int24 tickUpper,
uint128 amount
) external lock returns (uint256 amount0, uint256 amount1) {}
mint 函数定义内包含一个 lock 修饰器,该修饰器是为了避免重入的,其使用了 slot0 内的 unlocked 状态变量:
modifier lock() {
require(slot0.unlocked, 'LOK');
slot0.unlocked = false;
_;
slot0.unlocked = true;
}
接下来,我们所编写的代码都位于 mint 函数内部代码:
require(amount > 0);
(, int256 amount0Int, int256 amount1Int) = _modifyPosition(
ModifyPositionParams({
owner: recipient,
tickLower: tickLower,
tickUpper: tickUpper,
liquidityDelta: int256(uint256(amount)).toInt128()
})
);
amount0 = uint256(amount0Int);
amount1 = uint256(amount1Int);
if (amount0 > 0) {
IERC20(token0).transferFrom(msg.sender, address(this), amount0);
}
if (amount1 > 0) {
IERC20(token1).transferFrom(msg.sender, address(this), amount1);
}
此处的 _modifyPosition 函数内部实际上计算了铸造 amount 数量的 Uniswap V3 LP 所需要的 token0 和 token1 的数量。由于我们没有使用 uniswap v3 的回调方案,所以此处直接使用了 transferFrom 将固定数量的代币转移给池子。上述代码对于某些代币而言存在漏洞,建议用户不要在生产环境内使用。
在 Uniswap V3 的官方实现内,这部分使用了回调函数处理,但在本文中,我们并不会实现回调函数的相关逻辑。因为回调函数与 Uniswap v3 的外围合约存在一些依赖关系。
我们首先实现较为简单的 toInt128() 函数,该函数用于将 uint128 类型转化为 int128 类型。我们首先创建 clamm/src/libraries/SafeCast.sol 文件,并在该文件内输入以下内容:
// SPDX-License-Identifier: GPL-2.0-or-later
pragma solidity ^0.8.20;
library SafeCast {
function toInt128(int256 y) internal pure returns (int128 z) {
require((z = int128(y)) == y);
}
}
上述代码通过判断转化后的 z 和 y 是否一致来实现安全的类型转化。然后,我们需要在 CLAMM.sol 内使用 import "./libraries/SafeCast.sol"; 语句导入该库,并且使用 using SafeCast for int256; 语句将其使用在 int256 类型上。
在 mint 函数内,目前唯一没有实现的就是 _modifyPosition 函数,这是一个相当复杂的函数。本节后续所有内容都将围绕该函数展开。我们先给出该函数的定义:
function _modifyPosition(ModifyPositionParams memory params) private returns (Position.Info storage position, int256 amount0, int256 amount1) {}
在此定义内,我们会发现 ModifyPositionParams 结构体和 Position.Info 都没有此前进行过定义。所以第一步,我们先将这两个结构体进行定义。首先定义 ModifyPositionParams 结构体,该结构体用于传递用户流动性所在区间和流动性变化等参数。此处的 liquidityDelta 是 int128 类型,是因为我们在提取流动性时也会使用此结构体,此时的 liquidityDelta 就是负数,代表用户提取的流动性数量。
struct ModifyPositionParams {
// the address that owns the position
address owner;
// the lower and upper tick of the position
int24 tickLower;
int24 tickUpper;
// any change in liquidity
int128 liquidityDelta;
}
接下来,我们定义 Position.Info 结构体。创建 clamm/src/libraries/Position.sol 文件并写入以下内容。注意,在本节中,我们并不会涉及手续费计算问题,所以实际上只会使用 Info 中的 liquidity 参数。此处,我们也编写了 get 方法,该方法用于在存储映射内检索存储的结构体。
// SPDX-License-Identifier: GPL-2.0-or-later
pragma solidity ^0.8.20;
library Position {
struct Info {
// the amount of liquidity owned by this position
uint128 liquidity;
// fee growth per unit of liquidity as of the last update to liquidity or fees owed
uint256 feeGrowthInside0LastX128;
uint256 feeGrowthInside1LastX128;
// the fees owed to the position owner in token0/token1
uint128 tokensOwed0;
uint128 tokensOwed1;
}
function get(mapping(bytes32 => Info) storage self, address owner, int24 tickLower, int24 tickUpper)
internal
view
returns (Position.Info storage position)
{
position = self[keccak256(abi.encodePacked(owner, tickLower, tickUpper))];
}
}
然后,我们可以在 clamm/src/CLAMM.sol 主合约使用 import "./libraries/Position.sol"; 导入上述库,并使用以下代码创建相关存储映射:
using Position for Position.Info;
mapping(bytes32 => Position.Info) public positions;
using Position for mapping(bytes32 => Position.Info);
完成上述工作后,我们就可以编写 _modifyPosition 中的逻辑代码:
function _modifyPosition(ModifyPositionParams memory params)
private
returns (Position.Info storage position, int256 amount0, int256 amount1)
{
checkTicks(params.tickLower, params.tickUpper);
Slot0 memory _slot0 = slot0;
position = _updatePosition(
params.owner,
params.tickLower,
params.tickUpper,
params.liquidityDelta,
_slot0.tick
);
}
上述代码中,我们暂时缺失了 amount0 和 amount1 的计算,我们会在后文进行补充。
此处的 checkTicks 函数用于确定输入的参数是否正确,其具体实现如下:
function checkTicks(int24 tickLower, int24 tickUpper) private pure {
require(tickLower < tickUpper, "TLU");
require(tickLower >= TickMath.MIN_TICK, "TLM");
require(tickUpper <= TickMath.MAX_TICK, "TUM");
}
之后,我们可以看到 _modifyPosition 使用了 Slot0 memory _slot0 = slot0; 将位于存储内的 slot0 缓存到内存内部。如果读者希望更加深入的了解该优化的原理,可以参考笔者之前编写的 Solidity Gas 优化清单及其原理:存储、内存与操作符 一文。
而 _updatePosition 则较为复杂,我们将一步步构建,我们首先构造一个最简单的 _updatePosition 函数,实现如下:
function _updatePosition(address owner, int24 tickLower, int24 tickUpper, int128 liquidityDelta, int24 tick)
private
returns (Position.Info storage position)
{
position = positions.get(owner, tickLower, tickUpper);
// TODO: Fee
uint256 _feeGrowthGlobal0X128 = 0;
uint256 _feeGrowthGlobal1X128 = 0;
// TODO: Fee
position.update(liquidityDelta, 0, 0);
}
此处,我们跳过了所有的手续费计算环节,我们会在未来介绍此部分。此处使用了 position.update 函数,因为目前我们跳过了所有的手续费计算逻辑,所以 position.update 的唯一功能就是更新 position 内的 liquidity 字段。我们需要在 clamm/src/libraries/Position.sol 内编写如下函数:
function update(
Info storage self,
int128 liquidityDelta,
uint256 feeGrowthInside0X128,
uint256 feeGrowthInside1X128
) internal {
Info memory _self = self;
uint128 liquidityNext;
if (liquidityDelta == 0) {
require(_self.liquidity > 0, "0 liquidity");
liquidityNext = _self.liquidity;
} else {
liquidityNext = liquidityDelta < 0
? _self.liquidity - uint128(-liquidityDelta)
: _self.liquidity + uint128(liquidityDelta);
}
if (liquidityDelta != 0) self.liquidity = liquidityNext;
self.feeGrowthInside0LastX128 = feeGrowthInside0X128;
self.feeGrowthInside1LastX128 = feeGrowthInside1X128;
}
上述函数中需要注意的是:
- 在
liquidityDelta == 0且_self.liquidity == 0的情况下,不需要更新当前的position的liquidity字段 liquidity是一个uint128类型,但liquidityDelta是一个int128类型,我们需要手动处理当liquidityDelta < 0的情况
回到 _updatePosition 函数,接下来我们要在该函数内部完成 tick 部分的更新。tick 记录了流动性等信息,我们首先实现 tick 的结构体定义:
struct Info {
uint128 liquidityGross;
int128 liquidityNet;
uint256 feeGrowthOutside0X128;
uint256 feeGrowthOutside1X128;
bool initialized;
}
其中 liquidityGross 代表该 tick 内具有的流动性数量,该数值主要用于判断当前 tick 是否还存在流动性。initialized 表示当前 tick 是被初始化。feeGrowthOutside0X128 和 feeGrowthOutside1X128 用于计算手续费,我们目前并不会编写此部分代码。
而 liquidityNet 是一个重要的变量,该变量用于计算当前池子内活跃的流动性数量。liquidityNet 的运作原理非常有趣,我们可以观察下图(该图来自 Uniswap v3 详解(一):设计原理):
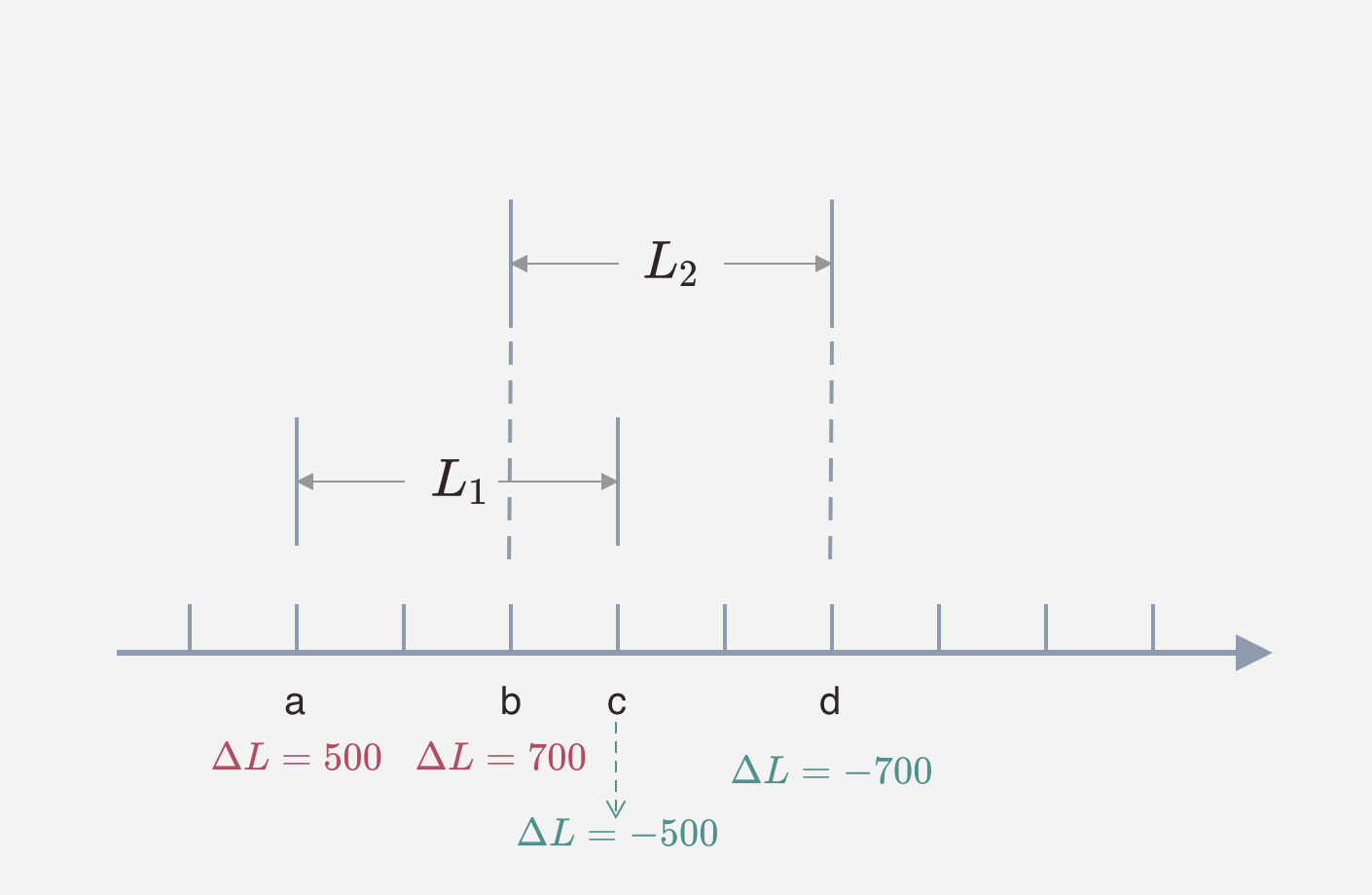
上图内显示了两段不同的区间流动性,其中 $L_1$ 是自 a tick 开始到 c tick 结束的价格区间,而 $L_2$ 是从 b tick 开始到 d tick 结束的价格区间。当用户添加 $L_1$ 流动性时,我们会在流动性区间的下限 a tick 的 liquidityNet 字段内记录添加的流动性数量 500,而在区间上限记录添加的流动性的相反数。让我们设想当起流动性池内启用了 L 单位流动性,且当前的价格为 p ,当价格 p 从 a 点的左侧移动到 a 点的右侧时,$L_1$ 所对应的流动性会被启用,此时池子内启用的流动性为 $L + 500$。当进一步向右移动超过 b 点时,池子内启用的流动性为 $L + 500 + 700 = L + 1200$。当价格进一步向右移动超过过 c 点时,$L_1$ 段流动性完全退出,此时直接使用 c 点记录的 liquidityNet = -500 就可以计算出当前池子内启用的流动性,数值为 $L + 1200 - 500 = L + 700$。当价格进一步向右移动超过 d 点时,$L_2$ 也退出,最终流动性变为 $L + 700 - 700 = L$。所以我们只需要记录修改价格区间的下限和上限就可以表示区间流动性。
接下来,我们把上述介绍的一些逻辑进行实现。我们先实现 tick 的更新函数,该函数定义如下:
function update(
mapping(int24 => Tick.Info) storage self,
int24 tick,
int24 tickCurrent,
int128 liquidityDelta,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128,
bool upper,
uint128 maxLiquidity
) internal returns (bool flipped) {}
此处我们删除了 Uniswap V3 原版代码内的预言机部分参数。该函数的返回值 flipped 代表更新后,tick 的状态是否有变化。当出现以下情况时,filpped 为 true:
update前,tick 的流动性,即liquidityGross参数为零值,但update后,liquidityGross不为零update前,tick 的流动性,即liquidityGross参数为非零值,但update后,liquidityGross为零
在有了上述函数定义后,我们开始编写函数的逻辑部分:
Tick.Info storage info = self[tick];
uint128 liuquidityGrossBefore = info.liquidityGross;
uint128 liquidityGrossAfter = liquidityDelta < 0
? liuquidityGrossBefore - uint128(-liquidityDelta)
: liuquidityGrossBefore + uint128(liquidityDelta);
require(liquidityGrossAfter <= maxLiquidity, "liquidity > max");
// flipped = (liuquidityGrossBefore == 0 && liquidityGrossAfter != 0)
// || (liuquidityGrossBefore != 0 && liquidityGrossAfter == 0);
flipped = (liquidityGrossAfter == 0) != (liuquidityGrossBefore == 0);
if (liuquidityGrossBefore == 0) {
info.initialized = true;
}
info.liquidityGross = liquidityGrossAfter;
info.liquidityNet = upper
? info.liquidityNet - liquidityDelta
: info.liquidityNet + liquidityDelta;
此处我们首先计算了 liquidityGrossAfter 即更新后的 tick 对应的流动性数值,然后计算了 flipped 变量。我们使用了异或运算简化了原有的 (liuquidityGrossBefore == 0 && liquidityGrossAfter != 0) || (liuquidityGrossBefore != 0 && liquidityGrossAfter == 0); 的复杂逻辑计算。本质原因是因为以下布尔计算的成立:
$$
p\oplus q=(p\lor q)\land (\lnot p\lor \lnot q)=(p+q)({\overline {p}}+{\overline {q}})
$$
在上述代码的最后,我们计算了最重要的 liquidityNet 参数。在 update 传参过程中,我们使用了 upper 标识是否为流动性区间上限。根据上文的推导,当 tick 位于某一流动性区间上限时,我们需要减去 liquidityDelta ,反之则加上 liquidityDelta。上述代码的最后一段就完成了此任务。
在 Tick.sol 内,我们还缺少一个移除 tick 的函数 clear,该函数相当简单:
function clear(mapping(int24 => Tick.Info) storage self, int24 tick) internal {
delete self[tick];
}
当我们完成上述 Tick.sol 内的代码后,我们首先在 clamm.sol 内导入上述定义和相关库函数:
using Tick for mapping(int24 => Tick.Info);
mapping(int24 => Tick.Info) public ticks;
然后,我们就可以继续完成我们的 _updatePosition 函数内部的 tick 更新逻辑:
function _updatePosition(address owner, int24 tickLower, int24 tickUpper, int128 liquidityDelta, int24 tick)
private
returns (Position.Info storage position)
{
position = positions.get(owner, tickLower, tickUpper);
// TODO: Fee
uint256 _feeGrowthGlobal0X128 = 0;
uint256 _feeGrowthGlobal1X128 = 0;
bool flippedLower;
bool flippedUpper;
if (liquidityDelta != 0) {
flippedLower = ticks.update(
tickLower,
tick,
liquidityDelta,
_feeGrowthGlobal0X128,
_feeGrowthGlobal1X128,
false,
maxLiquidityPerTick
);
flippedUpper = ticks.update(
tickUpper, tick, liquidityDelta, _feeGrowthGlobal0X128, _feeGrowthGlobal1X128, true, maxLiquidityPerTick
);
}
// TODO: Fee
position.update(liquidityDelta, 0, 0);
if (liquidityDelta < 0) {
if (flippedLower) {
ticks.clear(tickLower);
}
if (flippedUpper) {
ticks.clear(tickUpper);
}
}
}
此处,我们使用传入的 tickLower 和 tickUpper 来更新 ticks。并在最后使用 flippedLower 和 flippedUpper 的情况清空了不包含流动性的 tick。
至此,我们完成了 position 和 tick 的更新。position 用来表示用户添加的流动性区间的相关数据,而 tick 则主要用于存储流动性和手续费相关数据。
接下来,我们需要计算指定流动性所需要的代币数量。我们首先推导一下 Uniswap V3 的 AMM 曲线。首先,Uniswap V3 仍使用了 $x * y = L^2$ 的曲线,但是在 Uniswap V3 内存在区间流动性,最终造成了以下结果:
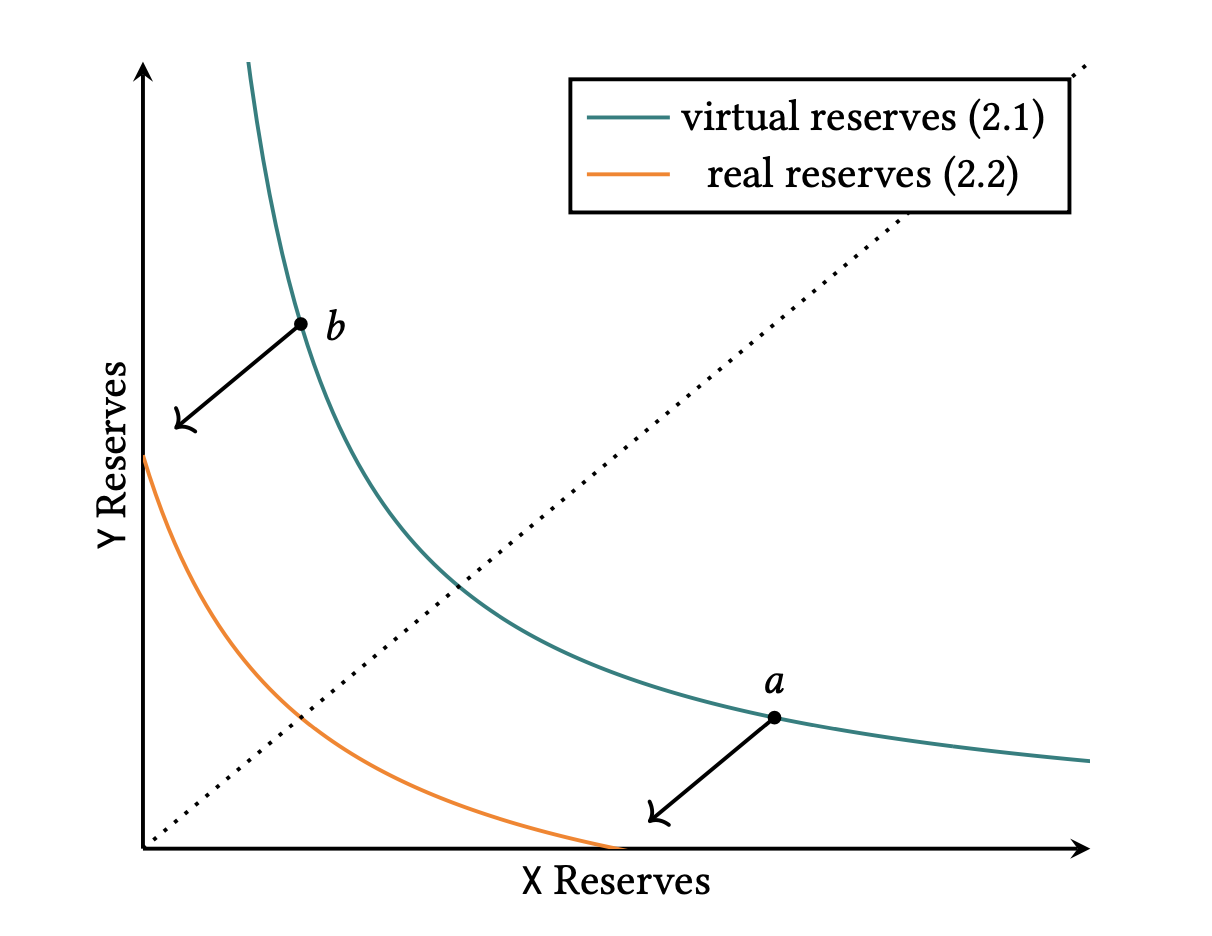
上图中的 virtual reserves 就是 Uniswap V3 曲线,但实际上 real reserves 才是真实情况。因为当价格位于 $P_b$ 时,区间内只存在 y 资产;而当价格位于 $P_b$ 时,区间内只存在 x 资产。我们需要建立价格 $P$ 与 $x$ 和 $y$ 代币数量的关系。在后文内,我们使用 $x_R$ 和 $y_R$ 代表当前区间内 $x$ 和 $y$ 代币的数量。

上图给出了更多的内容,以方便我们进行推导。其中靠近原点轴的曲线是实际代币构成的曲线,而远离原点的曲线则是在 AMM 计算过程中使用的 $x * y = L^2$ 的曲线。推导如下:
$$
\begin{align}
x * y &= L^2 \\
(x_R + x_v)(y_R + y_v) &= L^2 \\
\end{align}
$$
此时,我们不知道 $x_v$ 和 $y_v$ 的数值,我们需要借助 $x * y = L^2$ 和 $\frac{x}{y} = P$ 进行推导,可以获得如下等式:
$$
x = \frac{L}{\sqrt{P}} \\
y = L\sqrt{P}
$$
为了求解 $x_v$,我们计算当 $x_R = 0$ 的情况,此时 $P = P_B$:
$$
x_v(y_R + y_v) = x_v L\sqrt{P_B} = L^2 \\
x_v = \frac{L}{\sqrt{P_B}}
$$
同理,我们计算当 $y_R = 0$ 的情况,此时 $P = P_A$:
$$
(x_R + x_v)y_v = \frac{L}{P_A} y_v = L^2 \\
y_v = L\sqrt{P_A}
$$
最后,将上述计算获得 $x_v$ 和 $y_v$ 带入 $(x_R + x_v)(y_R + y_v) = L^2$ 可以获得如下结果:
$$
(x_R + \frac{L}{\sqrt{P_B}})(y_R + L\sqrt{P_A}) = L^2
$$
上述就是 AMM 曲线的最终形式,我们可以看到在此曲线内只使用了 $\sqrt{P}$ ,这也是为什么我们在上文最开始的 initialize 函数内要求用户输入 sqrtPriceX96 变量。接下来,我们需要推导在已知代币变化数量 $\Delta_x$ 或者 $\Delta_y$ 的情况下计算 $L$ 的数值。
我们首先计算 $P < P_A$ 的情况,此时区间内只存在数量为 $\Delta_x$ 的 x 资产,即 $y_R = 0$,所以我们可以得到以下等式: $$ (\Delta_x + \frac{L}{\sqrt{P_B}})L\sqrt{P_A} = L^2 \\ (\Delta_x + \frac{L}{\sqrt{P_B}})\sqrt{P_A} = L \\ \Delta_x = \frac{L}{\sqrt{P_A}} - \frac{L}{\sqrt{P_B}} \\ L = \frac{\Delta_x}{\frac{1}{\sqrt{P_A}} - \frac{1}{\sqrt{P_B}}} $$ 然后,我们计算 $P > P_B$ 的情况,此时区间内只存在数量为 $\Delta_y$ 的 y 资产,即 $x_R = 0$,所以我们得到以下等式: $$ \frac{L}{\sqrt{P_B}}(\Delta_y + L\sqrt{P_A}) = L^2 \\ \Delta_y = L \sqrt{P_B} - L\sqrt{P_A} \\ L = \frac{\Delta_y}{\sqrt{P_B} - \sqrt{P_A}} $$ 最后,我们计算 $P_A < P < P_B$ 的情况,此时我们将该区间分割为 $(P_A, P)$ 和 $(P, P_B)$ 的情况。对于 $(P_B, P)$ 情况内,我们可以视为 $P > P_B$ 的情况,只不过此处的 $P_A = P$ 。对于 $(P, P_A)$ 的情况,我们可以视为 $P < P_A$ 的情况,但是此处的 $P_A = P$。故而可以直接套用上述公式: $$ L = \frac{\Delta_x}{\frac{1}{\sqrt{P}} - \frac{1}{\sqrt{P_B}}} = \frac{\Delta_y}{\sqrt{P} - \sqrt{P_A}} $$ 此等式可以用于添加流动性时的计算,在已知添加 x 代币数量的情况下,计算需要添加的 y 代币数量。反之也可以计算。
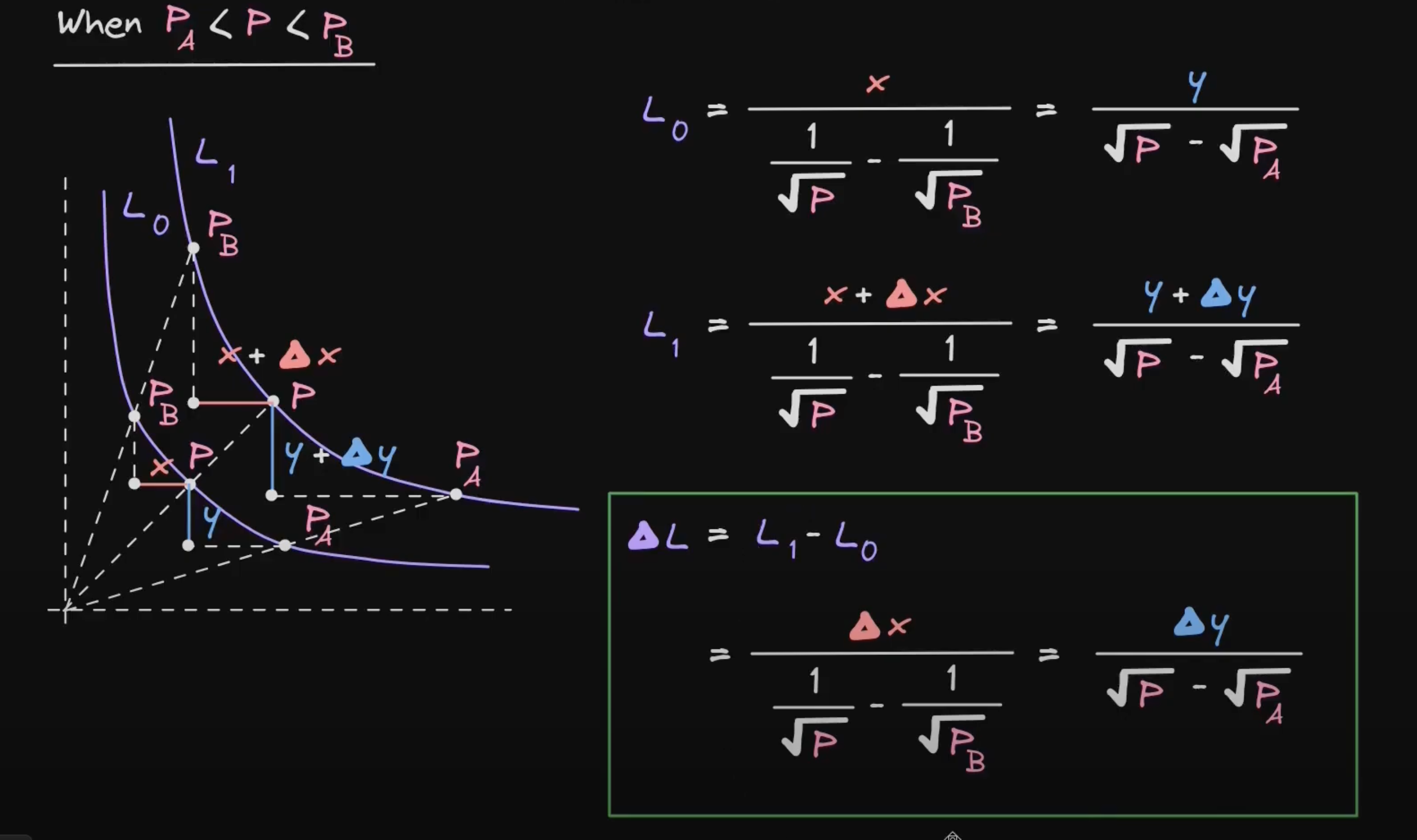
关于 $P_B < P < P_A$ 的情况,读者也可以使用下图理解:
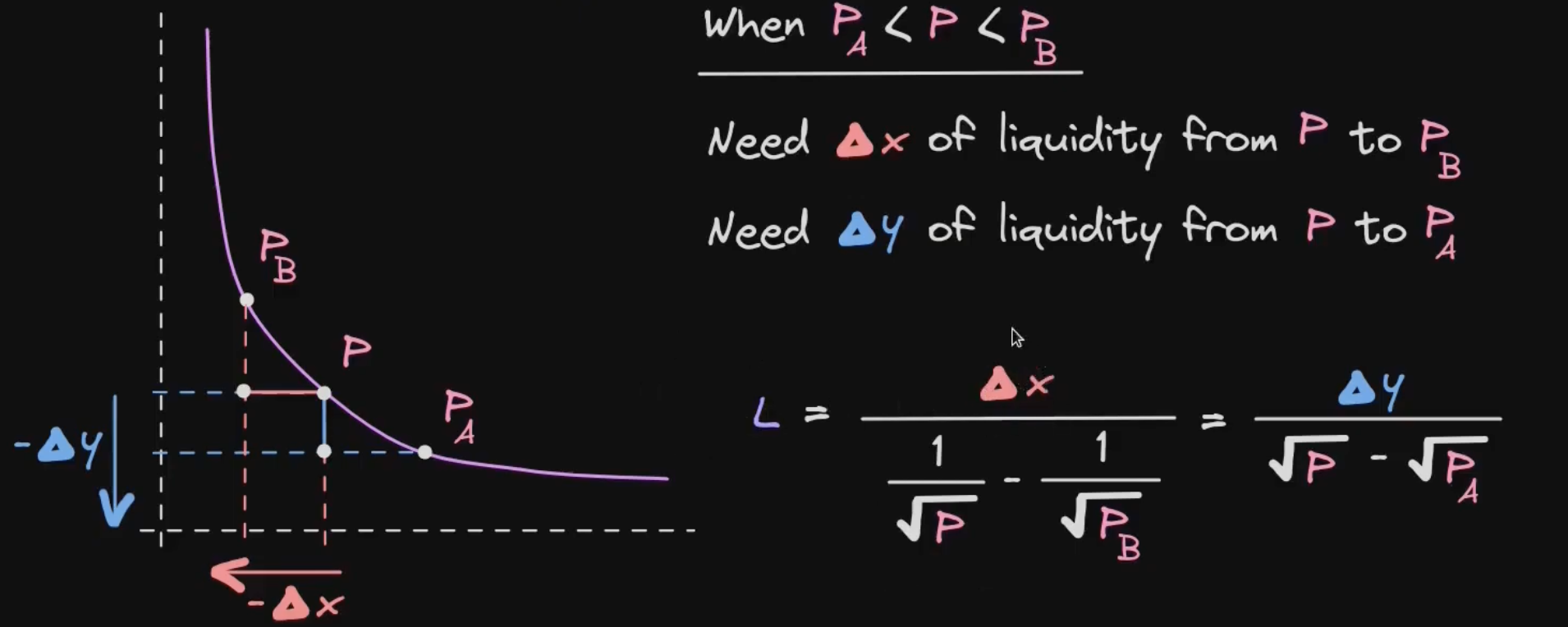
我们继续推导我们的目标,即在已知 $\Delta_L$ 的情况下,计算 $\Delta_x$ 和 $\Delta_y$ 。我们还是进行分情况讨论。
当 $P < P_A$ 时,我们可以看到
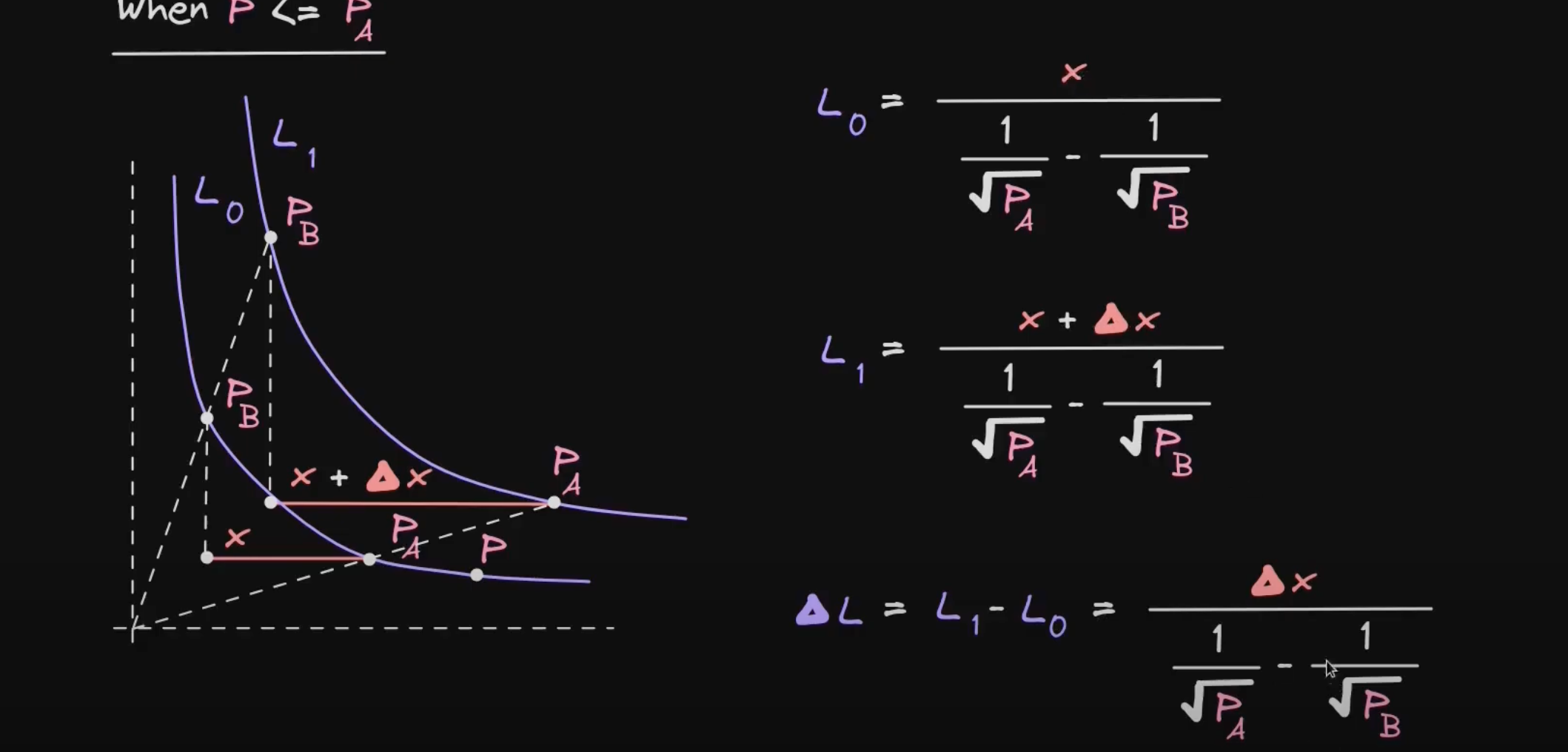
当 $P > P_B$ 时,我们可以推导: $$ L_0 = \frac{y}{\sqrt{P_B} - \sqrt{P_A}} \\ L_1 = \frac{y + \Delta_y}{\sqrt{P_B} - \sqrt{P_A}} \\ \Delta_y = L_1 - L_0 = \frac{\Delta_y}{\sqrt{P_B} - \sqrt{P_A}} $$ 当 $P_A < P <P_B$ 时,我们依旧是将原区间划分为两个区间来计算 $\Delta_x$ 和 $\Delta_y$,如下:
完成上述公式推导后,我们可以最终完成 _modifyPosition 函数,即该函数的计算指定流动性所需要的代币数量的部分。我们首先将上述公式在 clamm/src/libraries/SqrtPriceMath.sol 内实现,读者可以直接在 Uniswap 内直接将上述代码摘抄一下。此处的具体的实现读者可以自行参考相关代码。
此处我们可以讨论一下舍入问题,我们以 getAmount0Delta 为例:
function getAmount0Delta(uint160 sqrtRatioAX96, uint160 sqrtRatioBX96, int128 liquidity)
internal
pure
returns (int256 amount0)
{
return liquidity < 0
? -getAmount0Delta(sqrtRatioAX96, sqrtRatioBX96, uint128(-liquidity), false).toInt256()
: getAmount0Delta(sqrtRatioAX96, sqrtRatioBX96, uint128(liquidity), true).toInt256();
}
此处的调用的 getAmount1Delta(uint160 sqrtRatioAX96, uint160 sqrtRatioBX96, uint128 liquidity, bool roundUp) 的最后一个参数 roundUp 表示是否需要向上舍入。在此处,我们需要牢记一个原则,即所有误差都是由用户承担,流动性池不可以因为误差产生亏空。经过上文介绍,读者应该知道 getAmount0Delta 用于计算用户在指定流动性和价格的情况下,用户所需要的代币数量,所以此处我们在 liquidity >= 0 的情况下,选择向上舍入,要求用户支付更多代币;而在 liquidity < 0 的情况下,则放弃向上舍入,目标也是要求用户支付更多代币。
我们在 _modifyPosition 内按照上述描述的情况进行实现。
function _modifyPosition(ModifyPositionParams memory params)
private
returns (Position.Info storage position, int256 amount0, int256 amount1)
{
checkTicks(params.tickLower, params.tickUpper);
Slot0 memory _slot0 = slot0;
position = _updatePosition(params.owner, params.tickLower, params.tickUpper, params.liquidityDelta, _slot0.tick);
if (params.liquidityDelta != 0) {
if (_slot0.tick < params.tickLower) {
amount0 = SqrtPriceMath.getAmount0Delta(
TickMath.getSqrtRatioAtTick(params.tickLower),
TickMath.getSqrtRatioAtTick(params.tickUpper),
params.liquidityDelta
);
} else if (_slot0.tick > params.tickUpper) {
amount1 = SqrtPriceMath.getAmount1Delta(
TickMath.getSqrtRatioAtTick(params.tickLower),
TickMath.getSqrtRatioAtTick(params.tickUpper),
params.liquidityDelta
);
} else {
uint128 liquidityBefore = liquidity;
amount0 = SqrtPriceMath.getAmount0Delta(
_slot0.sqrtPriceX96, TickMath.getSqrtRatioAtTick(params.tickUpper), params.liquidityDelta
);
amount1 = SqrtPriceMath.getAmount1Delta(
TickMath.getSqrtRatioAtTick(params.tickLower), _slot0.sqrtPriceX96, params.liquidityDelta
);
liquidity = params.liquidityDelta < 0
? liquidityBefore - uint128(-params.liquidityDelta)
: liquidityBefore + uint128(params.liquidityDelta);
}
}
}
在此处,如果添加流动性的区间包括 _slot0.tick,此处会对 liquidity 进行修改。此处的 liquidity 指在当前价格下生效的流动性数量。
至此,我们就完成了流动性提供的所有流程。在此流程内,我们以此使用了以下函数:
_modifyPosition用来修改流动性提供区间的参数并计算指定流动性提供所需要的代币数量_updatePosition在_modifyPosition内部更新价格区间,目前我们实现了更新区间上限和下限 tick 的相关功能
流动性提取和收集
进行流动性的提取实际上就是 mint 函数的反向操作,我们可以直接使用 _modifyPosition 函数。此处,我们会使用到 Position.Info 内的 tokensOwed0 和 tokensOwed1 变量,该变量用于记录 Position 内部不作为流动性的代币。该函数实现如下:
function burn(int24 tickLower, int24 tickUpper, uint128 amount)
external
lock
returns (uint256 amount0, uint256 amount1)
{
(Position.Info storage position, int256 amount0Int, int256 amount1Int) = _modifyPosition(
ModifyPositionParams({
owner: msg.sender,
tickLower: tickLower,
tickUpper: tickUpper,
liquidityDelta: -int256(uint256(amount)).toInt128()
})
);
amount0 = uint256(-amount0Int);
amount1 = uint256(-amount1Int);
if (amount0 > 0 || amount1 > 0) {
(position.tokensOwed0, position.tokensOwed1) =
(position.tokensOwed0 + uint128(amount0), position.tokensOwed1 + uint128(amount1));
}
}
由于用户需要提取流动性,所以此处的 liquidityDelta 为 amount 的负数。在 burn 函数的最后,我们将输出的 amount0 和 amount1 添加到用户的 position 内部。
在上述流程内,我们并没有完成代币的提取。我们可以使用 collect 函数实现代币的提取,代码如下:
function collect(
address recipient,
int24 tickLower,
int24 tickUpper,
uint128 amount0Requested,
uint128 amount1Requested
) external lock returns (uint128 amount0, uint128 amount1) {
Position.Info storage position = positions.get(msg.sender, tickLower, tickUpper);
amount0 = amount0Requested > position.tokensOwed0 ? position.tokensOwed0 : amount0Requested;
amount1 = amount1Requested > position.tokensOwed1 ? position.tokensOwed1 : amount1Requested;
if (amount0 > 0) {
position.tokensOwed0 -= amount0;
IERC20(token0).transfer(recipient, amount0);
}
if (amount1 > 0) {
position.tokensOwed1 -= amount1;
IERC20(token1).transfer(recipient, amount1);
}
}
此处可以预告一下,在每次调用 _modifyPosition 时都会完成代表价格区间的 position 更新。在这部分更新过程中,我们会重新计算区间获得手续费情况,这部分手续费就会被记录在 position.tokensOwed0 和 position.tokensOwed1 内部。
Swap
swap 环节是 Uniswap 最复杂的环节之一,在本节内,我们将 swap 分为多个环节依次介绍。在 Uniswap 的白皮书内,给出了以下流程图:
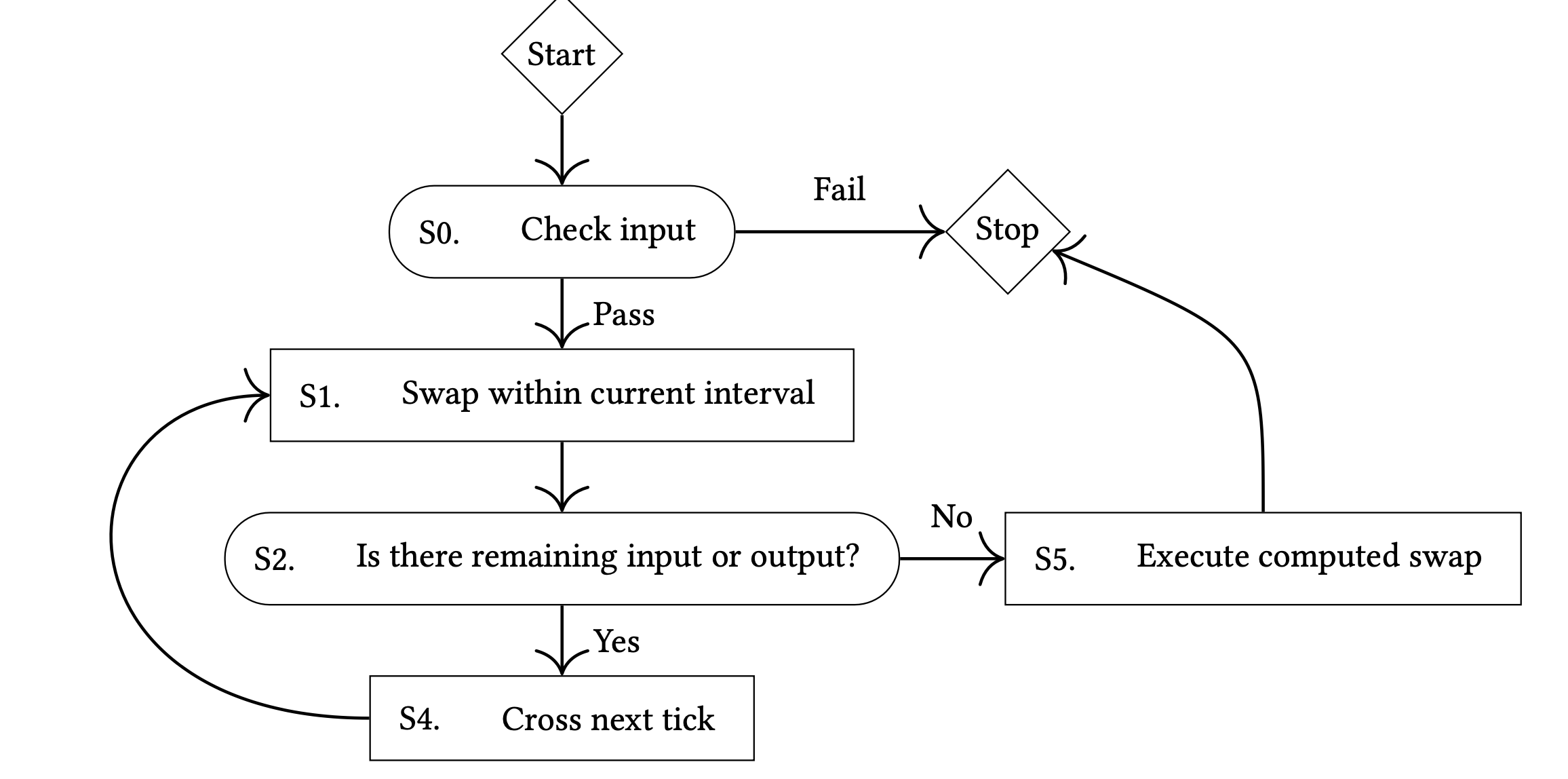
当用户的代币输入后,会在当前区间进行 swap 操作,然后检查是否完成了用户所有资金的兑换,如果没有,则寻找下一个价格区间继续进行兑换;如果已完成,则进行最终的代币转移。
computeSwapStep
我们先分析 computeSwapStep 函数,该函数的作用是在当前价格区间内进行代币的互换,该函数定义如下:
function computeSwapStep(
uint160 sqrtRatioCurrentX96,
uint160 sqrtRatioTargetX96,
uint128 liquidity,
int256 amountRemaining,
uint24 feePips
) internal pure returns (uint160 sqrtRatioNextX96, uint256 amountIn, uint256 amountOut, uint256 feeAmount) {
}
此函数的参数为:
sqrtRatioCurrentX96当前的池子内的价格sqrtRatioTargetX96当前的价格区间的下一个价格,我们现在可以认为该参数用于锁定价格区间,保证computeSwapStep只在某一区间内进行swap操作liquidity流动性,当前可用的流动性数量 $L$amountRemaining需要兑换的代币数量feePips手续费。Uniswap V3 使用 1e6 的精度保存手续费,即1e6 = 100%,而手续费的最小精度为0.01%。所以feePips = 1相当于0.01%的手续费。
返回值内的 sqrtRatioNextX96 代表当前 swap 结束后的价格,假如用户可以在当前区间完成所有兑换,则该价格就是兑换后价格;假如用户在当前区间无法完成所有代币兑换,则该价格会变成当前流动性区间的最大价格。而 amountIn 和 amountOut 则代表兑换的结果输出,在后文,我们会介绍为什么会有两个兑换结果的输出。而 feeAmount 则是当前兑换所需要的手续费。
由于 swap 内,大量涉及代币的顺序问题,在此处,我们可以认为以下几种说法是一致的:
token0/ $x$ 资产token1/ $y$ 资产
在 computeSwapStep 中的第一步是先确定兑换的方向,即是使用 token0 兑换 token1 还是使用 token1 兑换 token0。我们可以利用 computeSwapStep 输入的 sqrtRatioCurrentX96 和 sqrtRatioTargetX96 参数确定
我们可以推导出当 sqrtRatioCurrentX96 >= sqrtRatioTargetX96 时,应该为 token 0 -> token1,即:
bool zeroForOne = sqrtRatioCurrentX96 >= sqrtRatioTargetX96;
在 Uniswap V3 中,进行代币兑换有两种模式,一种是给定输入,要求将所有输入代币转化为输出代币,比如我们给定 1000 USDT 输入,要求 Uniswap V3 给定足够数量的 ETH 输出。另一种模式是给定输出,要求 Uniswap V3 基于我们的输出计算我的输入代币,比如给定我们需要兑换 1 ETH,要求 Uniswap V3 计算所吸引的 USDT 的数量。在实现上,给定输入还是给定输出取决于 amountRemaining 的正负情况。
当 amountRemaining >= 0 时,amountRemaining 等于输入代币的数量。
bool exactIn = amountRemaining >= 0;
接下来,我们可以分情况计算两种不同的模式。我们首先计算给定输入的情况,即 exactIn = true 的情况。我们首先需要知道当前区间所能接受的最大代币输入。即给定价格区间和流动性,计算当前流动性对应的代币数量。在上文介绍 _modifyPosition 时,我们已经介绍了 getAmount0Delta 和 getAmount1Delta 函数,这些函数刚好可以用来计算指定流动性下可以接受的最大代币数量。代码实现如下:
amountIn = zeroForOne
? SqrtPriceMath.getAmount0Delta(sqrtRatioTargetX96, sqrtRatioCurrentX96, liquidity, true)
: SqrtPriceMath.getAmount1Delta(sqrtRatioCurrentX96, sqrtRatioTargetX96, liquidity, true);
此处,需要注意 getAmount0Delta 要求第一个价格参数小于第二个价格参数,在此处,我们可以根据 zeroForOne 判断价格参数的大小。而且,注意 getAmount0Delta 计算是存在误差的,我们此处将 roundUp 设置为 true 使得用户承担误差。
接下来,我们要根据 amountIn 计算 swap 结束后的价格。此处也分为两种情况,第一种是在当前区间兑换没有全部完成,此时 swap 结束的价格就是当前价格区间的最大价格。我们可以根据 amountRemaining - fee >= amountIn 来判断。等同于我们支付了过多的输入代币,当前价格区间无法容纳。注意,我们在此处增加了手续费的计算。我们可以认为手续费是在用户的资金进入系统后立马扣除了,手续费部分不参与曲线上的计算。我们首先计算 amountRemaining - fee 的结果:
uint256 amountRemainingLessFee = FullMath.mulDiv(uint256(amountRemaining), 1e6 - feePips, 1e6);
然后,我们可以使用以下代码表示 amountRemainingLessFee >= amountIn 的情况,如下:
if (amountRemainingLessFee >= amountIn) {
sqrtRatioNextX96 = sqrtRatioTargetX96;
} else {
}
另一种情况时,在当前区间,用户所有的输入都被耗尽,此时我们需要计算价格。在此处,我们需要使用 amountRemainingLessFee 作为参数,因为手续费是一个 AMM 曲线外逻辑。代码如下:
if (amountRemainingLessFee >= amountIn) {
sqrtRatioNextX96 = sqrtRatioTargetX96;
} else {
sqrtRatioNextX96 = SqrtPriceMath.getNextSqrtPriceFromInput(
sqrtRatioCurrentX96, liquidity, amountRemainingLessFee, zeroForOne
);
}
此处我们直接调用了 getNextSqrtPriceFromInput 函数。该函数的具体计算原理是较为简单,我们可以使用上文给出的:
$$
L = \frac{\Delta_x}{\frac{1}{\sqrt{P_A}} - \frac{1}{\sqrt{P_B}}} \\
L = \frac{\Delta_y}{\sqrt{P_B} - \sqrt{P_A}}
$$
使用上述公式可以求解出:
$$
\frac{1}{\sqrt{P_A}} = \frac{1}{\sqrt{P}} + \frac{\Delta_x}{L} \\
\sqrt{P_B} = \sqrt{P} + \frac{\Delta_y}{L}
$$
也可以求解获得:
$$
\sqrt{P_A} = \frac{L\sqrt{P_B}}{L + x\sqrt{P_B}} \\
\sqrt{P_B} = \frac{L\sqrt{P_A}}{L - x\sqrt{P_A}}
$$
以及:
$$
\sqrt{P_A} = \sqrt{P_B} - \frac{y}{L} \\
\sqrt{P_B} = \sqrt{P_A} + \frac{y}{L}
$$
所以,我们可以在已知 liquidity / sqrtRatioCurrentX96 和 amountRemainingLessFee 的情况下计算出价格。
接下来,我们处理另一种情况,即 amountRemaining 数值代表代币输出数量的情况。
amountOut = zeroForOne
? SqrtPriceMath.getAmount1Delta(sqrtRatioTargetX96, sqrtRatioCurrentX96, liquidity, false)
: SqrtPriceMath.getAmount0Delta(sqrtRatioCurrentX96, sqrtRatioTargetX96, liquidity, false);
我们还是首先计算在当前流动性下,可以输出的最大代币数量。当用户选择 token 0 -> token 1 时,即 zeroForOne = true 时,此时我们使用 getAmount1Delta 计算 token1 的数量。相反,当用户选择 token 1 -> token 0 时,我们使用 getAmount0Delta 计算 token 0 的数量。此处,我们没有将 roundUp 置为 true,是因为此时计算出的输出应该向下取整,避免用户获得更多的代币。
之后,我们依旧需要判断当前区间是否可以完成这笔兑换:
if (uint256(-amountRemaining) >= amountOut) {
sqrtRatioNextX96 = sqrtRatioTargetX96;
} else {
sqrtRatioNextX96 = SqrtPriceMath.getNextSqrtPriceFromOutput(
sqrtRatioCurrentX96, liquidity, uint256(-amountRemaining), zeroForOne
);
}
此处的代码也适用于计算 sqrtRatioNextX96 变量。在当前区间无法完成兑换时,直接将 sqrtRatioNextX96 置为 sqrtRatioTargetX96。反之,则使用流动性等因子计算价格。
接下来,我们需要计算真正的 amountIn 和 amountOut。在上文内,我们计算出的 amountIn 或者 amountOut 实际上都是在假设完全消耗区间流动性的情况下计算出的。而实际情况不一定消耗了所有的区间流动性。我们首先使用以下代码计算当前是否属于区间流动性被耗尽的情况:
bool max = sqrtRatioTargetX96 == sqrtRatioNextX96;
之后,我们可以分情况进行讨论:
max = true && exactIn = true的情况。此时等同于区间流动性被耗尽,此时amountIn可以直接使用,但输出amountOut需要单独计算max = true && exactIn = False的情况。此amountOut可以直接使用,但amountIn需要单独计算- 其他情况下,由于区间流动性没有被耗尽,我们之前计算出的
amountIn和amountOut都没有作用,所以我们都需要重新计算
我们首先计算在 zeroForOne = true 的情况下,amountIn 和 amountOut 的数值:
amountIn = max && exactIn
? amountIn
: SqrtPriceMath.getAmount0Delta(sqrtRatioNextX96, sqrtRatioCurrentX96, liquidity, true);
amountOut = max && !exactIn
? amountOut
: SqrtPriceMath.getAmount1Delta(sqrtRatioNextX96, sqrtRatioCurrentX96, liquidity, false);
当 max && exactIn 都成立的情况下,amountIn 的数值为 amountIn ,否则就需要使用更新后的 sqrtRatioNextX96 进行计算。amountOut 同理。
然后,我们需要计算 zeroForOne = false 的情况下的 amountIn 和 amountOut 的数值:
amountIn = max && exactIn
? amountIn
: SqrtPriceMath.getAmount1Delta(sqrtRatioCurrentX96, sqrtRatioNextX96, liquidity, true);
amountOut = max && !exactIn
? amountOut
: SqrtPriceMath.getAmount0Delta(sqrtRatioCurrentX96, sqrtRatioNextX96, liquidity, false);
最后,我们需要限制 amountOut 的输出数值,如下:
if (!exactIn && amountOut > uint256(-amountRemaining)) {
amountOut = uint256(-amountRemaining);
}
这是为了防止计算出现误差,导致合约输出了大于用户要求的代币数量。这个误差会发生在 !exactIn && !max 的情况下,此时我们会使用 sqrtRatioNextX96 = SqrtPriceMath.getNextSqrtPriceFromOutput(sqrtRatioCurrentX96, liquidity, uint256(-amountRemaining), zeroForOne ); 计算下一个价格,然后使用 getAmount0Delta 和 getAmount1Delta 计算真正的输入和输出。在此环节内,由于 sqrtRatioNextX96 可能存在误差,导致计算出的 amountOut 稍大于 uint256(-amountRemaining)。
最后,我们完成手续费的计算。手续费的计算需要以下推导:
$$
x = a + fee = a + x * f \\
x = \frac{a}{1 - f} \\
fee = x * f = \frac{af}{1 - f}
$$
上述公式内的 a 代表不带手续费的代表输入,$x$ 代表包含手续费的代币输入,$f$ 代表手续费率。基于上述推导,我们可以得到以下代码:
if (exactIn && sqrtRatioNextX96 != sqrtRatioTargetX96) {
feeAmount = uint256(amountRemaining) - amountIn;
} else {
feeAmount = FullMath.mulDivRoundingUp(amountIn, feePips, 1e6 - feePips);
}
此处,我们简化了部分计算。即当用户给定输入代币数量并且 swap 后价格没有移动到价格区间外时,我们直接将用户所有输入减去 amountIn 的部分作为手续费。这实际上也是让用户承担误差的一种手段。
swap 非核心代码
在本节中,我们将分析 swap 函数中的参数校验部分,也是本节开始时给出的流程图中的 S0 环节。我们依旧先给出 swap 的函数定义:
function swap(address recipient, bool zeroForOne, int256 amountSpecified, uint160 sqrtPriceLimitX96)
external
returns (int256 amount0, int256 amount1)
{}
swap 函数的 recipient 参数表示代币兑换后的接收方。zeroForOne 表示代币兑换的方向,当 zeroForOne = true 时,代表用户是使用 token 0 兑换 token 1 ,反之则表示用户使用 token 1 兑换 token 0。amountSpecified 表示代币兑换的数量,当该数值为正时,代表用户给定了输入代币的数量,要求池子给出输出代币的数量;当该数值为负时,代表用户给定了输出代币的数量,要求池子给出输入代币的数量。sqrtPriceLimitX96 用于限定兑换价格,当兑换价格到达 sqrtPriceLimitX96 时,swap 就会终止。
除此外,Uniswap V3 定义了一系列结构体用于 swap 过程中缓存数据。定义如下:
struct SwapCache {
// liquidity at the beginning of the swap
uint128 liquidityStart;
}
struct SwapState {
// the amount remaining to be swapped in/out of the input/output asset
int256 amountSpecifiedRemaining;
// the amount already swapped out/in of the output/input asset
int256 amountCalculated;
// current sqrt(price)
uint160 sqrtPriceX96;
// the tick associated with the current price
int24 tick;
// the global fee growth of the input token
uint256 feeGrowthGlobalX128;
// the current liquidity in range
uint128 liquidity;
}
struct StepComputations {
// the price at the beginning of the step
uint160 sqrtPriceStartX96;
// the next tick to swap to from the current tick in the swap direction
int24 tickNext;
// whether tickNext is initialized or not
bool initialized;
// sqrt(price) for the next tick (1/0)
uint160 sqrtPriceNextX96;
// how much is being swapped in in this step
uint256 amountIn;
// how much is being swapped out
uint256 amountOut;
// how much fee is being paid in
uint256 feeAmount;
}
这些结构体都会在 swap 过程中使用。我们首先校验 amountSpecified 参数,该参数不应该为 0,因为该参数表示兑换的代币数量。对应的校验代码如下:
require(amountSpecified != 0, "AS");
为了避免重入攻击,此处我们也需要校验重入锁部分:
Slot0 memory slot0Start = slot0;
require(slot0Start.unlocked, "LOK");
然后,我们校验 sqrtPriceLimitX96 参数,该参数的取值取决于 OneForZero 参数。我们再次给出上文的结论:当 sqrtRatioCurrentX96 >= sqrtRatioTargetX96 时,应该为 token 0 -> token1。所以,我们可以获得以下结论:
require(
zeroForOne
? sqrtPriceLimitX96 < slot0Start.sqrtPriceX96 && sqrtPriceLimitX96 > TickMath.MIN_SQRT_RATIO
: sqrtPriceLimitX96 > slot0Start.sqrtPriceX96 && sqrtPriceLimitX96 < TickMath.MAX_SQRT_RATIO,
'SPL'
);
即当 zeroForOne = true 时,sqrtPriceLimitX96 应该小于当前的价格 slot0Start.sqrtPriceX96,但是需要大于最小价格;当 zeroForOne = false 时,sqrtPriceLimitX96 应该大于当前价格 slot0Start.sqrtPriceX96,但应当小于最大价格。
完成上述校验后,我们最后将重入锁重新锁定:
slot0.unlocked = false;
完成上述的入参校验后,我们将相关数据缓存到上文给出的价格结构体内部:
SwapCache memory cache = SwapCache({liquidityStart: liquidity});
bool exactInput = amountSpecified > 0;
SwapState memory state = SwapState({
amountSpecifiedRemaining: amountSpecified,
amountCalculated: 0,
sqrtPriceX96: slot0Start.sqrtPriceX96,
tick: slot0Start.tick,
feeGrowthGlobalX128: zeroForOne ? feeGrowthGlobal0X128 : feeGrowthGlobal1X128,
liquidity: cache.liquidityStart
});
在此处,我们完成了 SwapCache 和 SwapState 的初始化。在 SwapState 内,amountCalculated 代表在当前兑换过程中,所需要的另一种代币数量,该数值会不断累积。而 feeGrowthGlobalX128 则用于缓存当前的手续费情况,并会在 swap 过程中不断更新。上述缓存内的大部分数据我们最终都需要写回存储内部。
在完成上述数据缓存后,swap 函数会进入真正的兑换流程。兑换流程是一个循环操作,首先找到可用的流动性区间,然后在可用的流动性区间内调用我们上文编写的 computeSwapStep 函数进行兑换操作,在完成兑换操作后更新缓存内的数据,并最终判断是否需要跳出循环。该部分代码较为复杂,我们会在下一节介绍。
当上述 swap 循环完成后,缓存中的数据需要同步到存储内部,本节将继续介绍缓存写回存储的相关代码。代码如下:
// Update slot0 tick and sqrtPriceX96
if (state.tick != slot0Start.tick) {
(slot0.sqrtPriceX96, slot0.tick) = (state.sqrtPriceX96, state.tick);
} else {
slot0.sqrtPriceX96 = state.sqrtPriceX96;
}
// Update liquidity
if (cache.liquidityStart != state.liquidity) liquidity = state.liquidity;
// Update fee growth
if (zeroForOne) {
feeGrowthGlobal0X128 = state.feeGrowthGlobalX128;
} else {
feeGrowthGlobal1X128 = state.feeGrowthGlobalX128;
}
结束上述的缓存写回流程后,我们继续完成 swap 的最后逻辑,实现代币的转移。对于代币的转移,我们存在以下几种情况:
exactIn = true && zeroForOne = true此时amount 0 = amountSpecified - amountSpecifiedRemaining。原因在于当指定token 0数量时,可能即使兑换到用户指定的极限目标价格(sqrtPriceLimitX96) 仍无法完成全部兑换。而amount 1 = amountCalculatedexactIn = true && zeroForOne = false此时等同于exactIn = true && zeroForOne = true的反向操作,所以 ``amount 0 = amountCalculated且amount 0 = amountSpecified - amountSpecifiedRemaining`exactIn = false && zeroForOne = true等同于exactIn = true && zeroForOne = false,所以amount 0 = amountCalculated且amount 0 = amountSpecified - amountSpecifiedRemainingexactIn = false && zeroForOne = false实际上等同于exactIn = true && zeroForOne = true的情况,因为此时也是使用 token 0 兑换 token 1 的场景
我们也可以使用以下表格归纳:
// Set amount0 and amount1
// zero for one | exact input |
// true | true | amount 0 = specified - remaining (> 0)
// | | amount 1 = calculated (< 0)
// false | false | amount 0 = specified - remaining (< 0)
// | | amount 1 = calculated (> 0)
// false | true | amount 0 = calculated (< 0)
// | | amount 1 = specified - remaining (> 0)
// true | false | amount 0 = calculated (> 0)
// | | amount 1 = specified - remaining (< 0)
关于以上表格内部的 > 0 或者 < 0 的关系,我们可以非常简单的使用 bool exactInput = amountSpecified > 0; 的条件进行判断。当 exactInput = true 时,那么 amountSpecified > 0,最终计算出的结果也大于 0。反之,则小于 0。综上所述,我们可以得到以下结论:
(amount0, amount1) = zeroForOne == exactInput
? (amountSpecified - state.amountSpecifiedRemaining, state.amountCalculated)
: (state.amountCalculated, amountSpecified - state.amountSpecifiedRemaining);
最后,我们完成代币的转移,具体代码如下:
if (zeroForOne) {
if (amount1 < 0) {
IERC20(token1).transfer(recipient, uint256(-amount1));
IERC20(token0).transferFrom(address(msg.sender), recipient, uint256(amount0));
}
} else {
if (amount0 < 0) {
IERC20(token0).transfer(recipient, uint256(-amount0));
IERC20(token1).transferFrom(address(msg.sender), recipient, uint256(amount1));
}
}
此处需要注意 amount1 amount0 与 0 之间的关系,在上文给出的表格内,我们已经给出了相关关系。
初试核心循环
正如上文所述,swap 的核心部分是一个循环,该循环不断寻找符合要求的含有流动性的区间使用 computeSwapStep 进行兑换操作,兑换完成后更新数据,然后进行一步决定是否继续循环还是跳出循环进入最终的结算环节。
我们首先编写循环的条件:
while (state.amountSpecifiedRemaining != 0 && state.sqrtPriceX96 != sqrtPriceLimitX96) {}
此处的 amountSpecifiedRemaining 是指用户给定代币的剩余数量。在 swap 过程中,每进行一次 swap ,我们都会在该数值内减去 swap 已经消耗的代币,所以当 state.amountSpecifiedRemaining != 0 时,说明用户仍存在代币未被兑换,此时可以继续循环。而 sqrtPriceLimitX96 是用户指定的兑换价格的极限,如果当前价格 state.sqrtPriceX96 没有达到 sqrtPriceLimitX96 ,我们可以考虑继续循环。但是当两者中,任意一个条件被满足,我们就需要跳出循环。
在本节内部,我们不会完成核心循环的所有逻辑,我们只会介绍核心循环的第一次循环。因为核心循环依赖于其他较为复杂的库函数,这些库函数我们会在下文进行介绍。我们首先编写第一次循环过程中的基础代码:
StepComputations memory step;
step.sqrtPriceStartX96 = state.sqrtPriceX96;
step.tickNext = zeroForOne ? state.tick - 1 : state.tick + 1;
if (step.tickNext < TickMath.MIN_TICK) {
step.tickNext = TickMath.MIN_TICK;
} else if (step.tickNext > TickMath.MAX_TICK) {
step.tickNext = TickMath.MAX_TICK;
}
step.sqrtPriceNextX96 = TickMath.getSqrtRatioAtTick(step.tickNext);
在此部分代码内,我们直接假设 step.tickNext 就是当 state.tick 的下一个 tick。我们会在后文引入 bitmap 进行下一个流动性区间的搜索,但在此处,我们直接使用了一个 mock 数值。当然,我们需要保证 step.tickNext 在预期的 tick 范围内部。
接下来,我们需要在流动性区间内调用 computeSwapStep 函数进行相关计算。在 computeSwapStep 函数内部,我们需要输入 sqrtRatioTargetX96 变量,此变量较为复杂,具有以下几种情况:
- 当
zeroForOne = true时,sqrtRatioTargetX96 = max(next, limit) - 当
zeroForOne = false时,sqrtRatioTargetX96 = min(next, limit)
我们最终可以获得如下代码:
(state.sqrtPriceX96, step.amountIn, step.amountOut, step.feeAmount) = SwapMath.computeSwapStep(
state.sqrtPriceX96,
(zeroForOne ? step.sqrtPriceNextX96 < sqrtPriceLimitX96 : step.sqrtPriceNextX96 > sqrtPriceLimitX96)
? sqrtPriceLimitX96
: step.sqrtPriceNextX96,
state.liquidity,
state.amountSpecifiedRemaining,
fee
);
对于最为复杂的 sqrtRatioTargetX96 的三目表达式计算,我们可以展开为:
- 在
zeroForOne = true的情况下step.sqrtPriceNextX96 < sqrtPriceLimitX96成立,此时返回sqrtPriceLimitX96,step.sqrtPriceNextX96 > sqrtPriceLimitX96成立,此时返回step.sqrtPriceNextX96
- 在
zeroForOne = false的情况下step.sqrtPriceNextX96 < sqrtPriceLimitX96成立,此时返回step.sqrtPriceNextX96step.sqrtPriceNextX96 > sqrtPriceLimitX96成立,此时返回sqrtPriceLimitX96
上述三目表达式实际上就是以上四种情况的总结版本。然后,我们根据计算结果更新状态变量:
if (exactInput) {
state.amountSpecifiedRemaining -= (step.amountIn + step.feeAmount).toInt256();
state.amountCalculated -= step.amountOut.toInt256();
} else {
state.amountSpecifiedRemaining += step.amountOut.toInt256();
state.amountCalculated += (step.amountIn + step.feeAmount).toInt256();
}
此处当 exactInput = true 时,我们可以知道 state.amountSpecifiedRemaining > 0,所以我们需要减去兑换消耗的 step.amountIn 和 step.feeAmount。当 exactInput = false 时,我们可以知道 state.amountSpecifiedRemaining < 0,所以我们会使用 step.amountOut 进行相加操作,对于 state.amountCalculated 也同理。
由于本节只是初步介绍,所以跳过了 step.nextTick 的计算和跨区间的流动性修改的部分函数。
BitMap
在上文内,我们介绍如何 swap 的基础原理,但我们没办法寻找到下一个区间。在本文内,我们将引入 BitMap 来进行流动性区间的搜索。一种朴素的搜索流动性区间的方案是遍历每一个 tick 来查询是否存在流动性。但我们的 tick 区间为 $[−887272,887272]$,这是一个相当大的区间,即是小范围的检索也需要消耗大量 gas。所以,我们引入了 tickSpacing 参数来进行跳跃的 tick 检索。
接下来,我们只需要将 $[−887272,887272]$ 范围内的所有 tick 填充到一个位图内即可。如果将总计 1774545 个 tick 填充到位图内部,我们需要 1774545 bit 的长度。显然,solidity 原生无法一次存储如此大的空间。所以,我们使用了映射进行存储:
mapping(int24 => Tick.Info) public ticks;
mapping(int16 => uint256) public tickBitmap;
我们将 int24 的 tick 分割为 int16 + uint8 ,其中 int16 被称为 word position,该参数也用作 tickBitmap 的键,而后 uint8 被称为 bit position,该参数被用作 tickBitmap 的值。我们可以认为 tickBitmap 就是一个如下的长位图:

对于 tick 的 int24 分割,我们可以使用以下代码处理(该代码位于 clamm/src/libraries/TickBitmap.sol 内部):
function position(int24 tick) private pure returns (int16 wordPos, uint8 bitPos) {
wordPos = int16(tick >> 8);
bitPos = uint8(uint24(tick % 256));
}
我们使用位移获得前 8 bit 作为 wordPos,使用模除获得后 8 bit 作为 bitPos。
接下来,我们讨论在已知 ticks 的情况下,如何将其存储到 tickBitmap 内部。
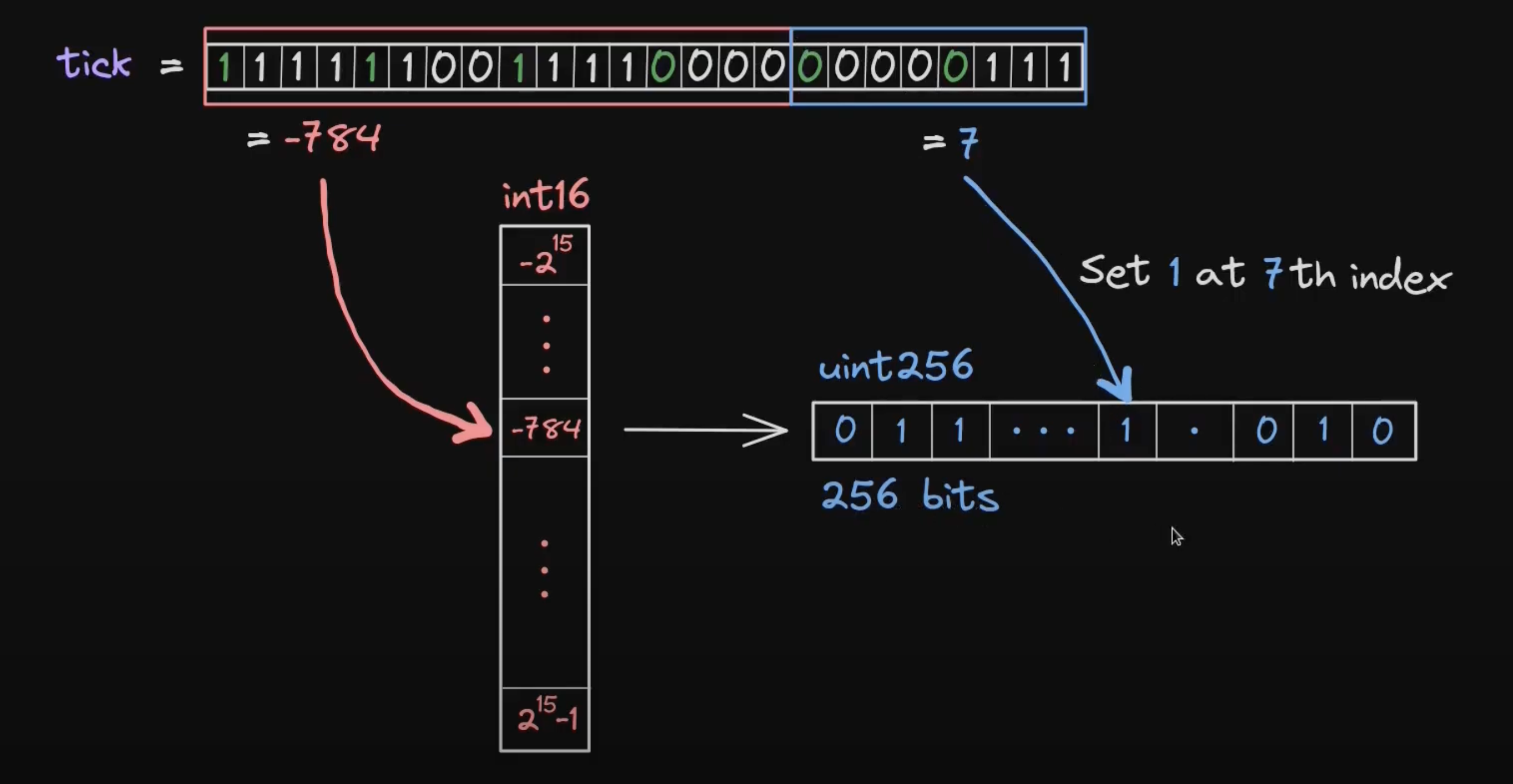
我们首先将一个 tick 划分为 int16 + uint8 ,其中 int16 部分作为 tickBitmap 的键,而 uint8 部分则转化为指定位置的位元写入 tickBitmap 的 uint256 值内部。由于 uint8 最大数值为 255,所以 uint256 是有足够空间储存的。在具体的写入流程内,我们会使用 mask 掩码方案进行写入。
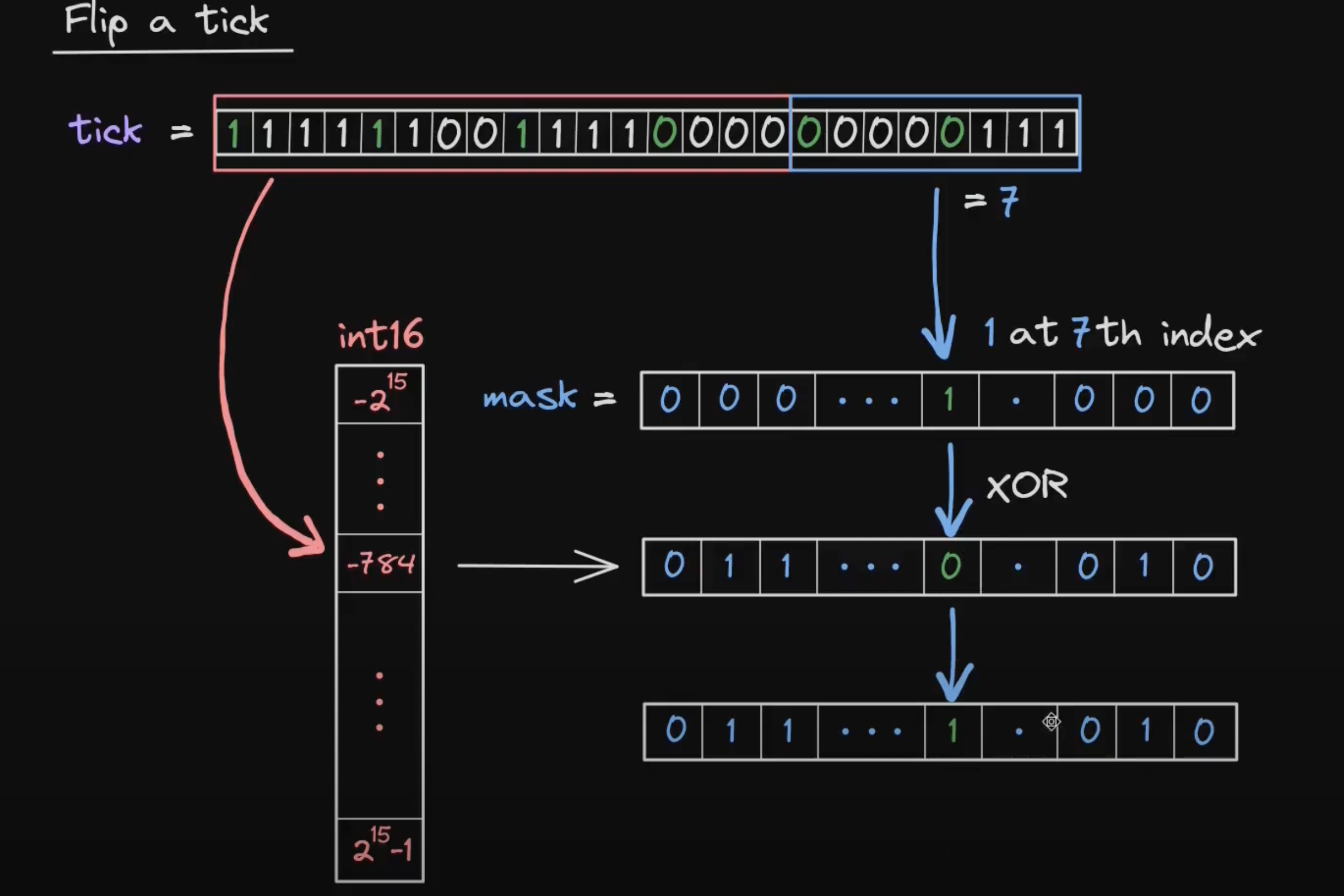
而读取数据的过程就是上述写入流程的逆过程,较为简单。
存储部分可以使用以下代码实现。但需要注意,存储需要考虑 tickSpacing 的影响。我们会将当前的 tick 放缩到 tickSpacing 内部成立的 tick。
function flipTick(
mapping(int16 => uint256) storage self,
int24 tick,
int24 tickSpacing
) internal {
require(tick % tickSpacing == 0);
(int16 wordPos, uint8 bitPos) = position(tick / tickSpacing);
uint256 mask = 1 << bitPos;
self[wordPos] ^= mask;
}
介绍完 bitmap 内的读取和写入后,我们希望进一步探索如何寻找下一个被初始化的 tick。这个问题等同于寻找离当前 tick 对应的 Index 左侧或则右侧的非零位元。
我们先介绍如何寻找小于当前 tick 的 nextTick,等同于寻找当前 tick 的右侧位元。此过程可以使用下图展示:
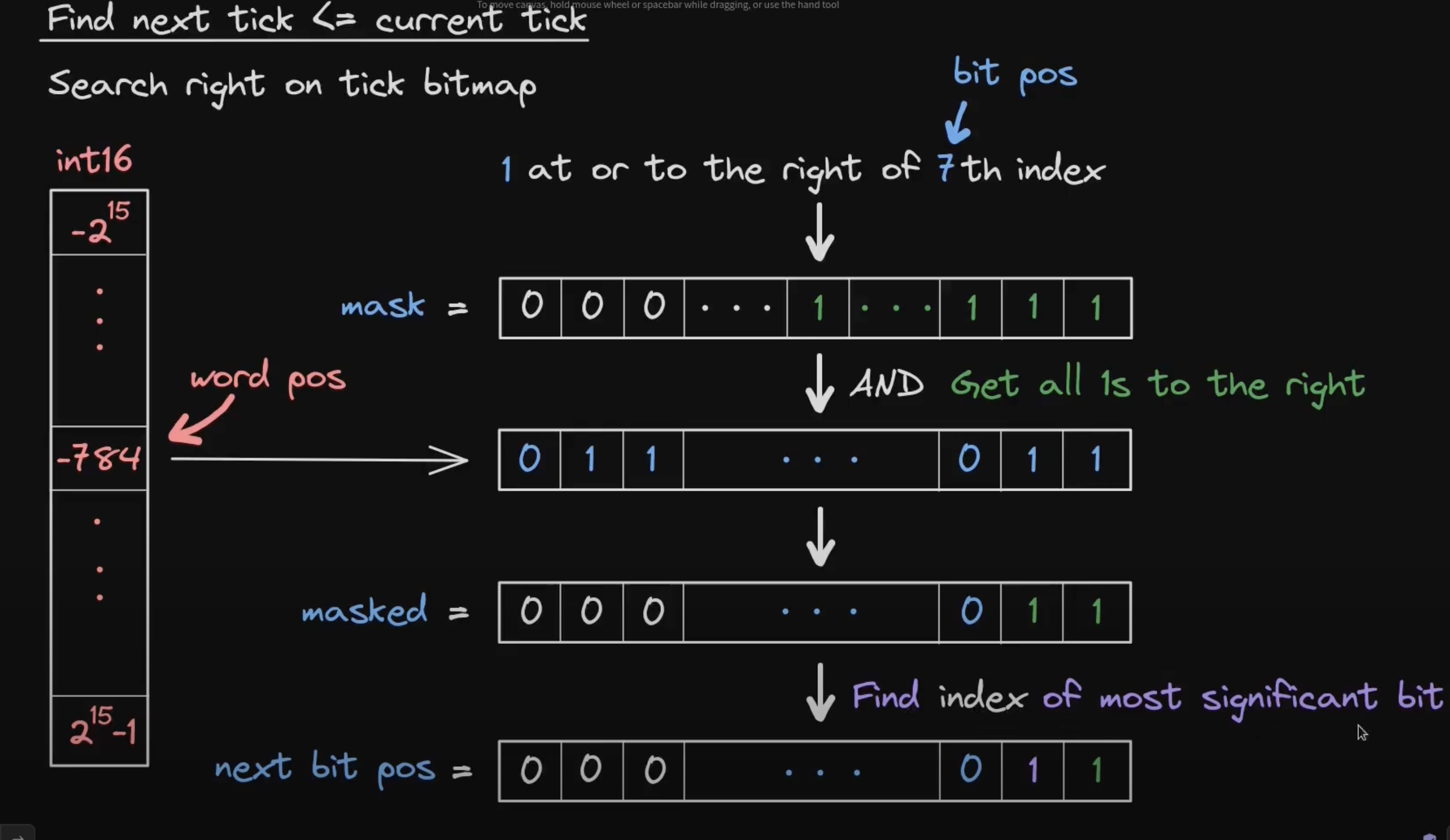
此处的 Find index of most significant bit 就是搜索当前位图内部最大的位元,该位元也是离当前 tick 最近的右侧位元。在代码内,该函数被命名为 mostSignificantBit。具体实现上,一般使用二分法快速获得当前位图内最大的位元。在此处 next bit pos 等于当前位元距离零索引的距离。我们会发现由于寻找的是左侧位元,所以即使 masked 内包含当前 tick 依旧不会有任何问题。当我们找到当前位图内最大的位元后,我们使用以下算法计算新的的 tick 的位置:
next tick = tick - bit pos + next bit pos
上述描述可以使用以下代码表示:
function nextInitializedTickWithinOneWord(
mapping(int16 => uint256) storage self,
int24 tick,
int24 tickSpacing,
bool lte
) internal view returns (int24 next, bool initialized) {
int24 compressed = tick / tickSpacing;
if (tick < 0 && tick % tickSpacing != 0) compressed--;
if (lte) {
(int16 wordPos, uint8 bitPos) = position(compressed);
uint256 mask = (1 << bitPos) - 1 + (1 << bitPos);
uint256 masked = self[wordPos] & mask;
initialized = masked != 0;
next = initialized
? (compressed - int24(uint24(bitPos - BitMath.mostSignificantBit(masked)))) * tickSpacing
: (compressed - int24(uint24(bitPos))) * tickSpacing;
} else {}
}
此处的 lte 分支内的代码就是上述介绍的寻找当前 tick 左侧的 tick 的代码。这里需要注意,由于我们使用了基于 tickSpacing 压缩的 tick 索引,所以在函数最开始就需要计算压缩后的 tick 索引 compressed。这里还需要注意我们都是选择向下取整来压缩 tick。但是对于负数而言,使用除法会出现向上取整的情况,所以此处使用了 if (tick < 0 && tick % tickSpacing != 0) compressed--; 来避免除法的向上取整。
为什么此处要保持向下取整,是因为对于 $[-1, 1]$ 的区间而言,如果我们不保持向零取整,那么就会导致两侧的重叠。
此处,为了构造当前 tick 右侧均为 1 的的掩码,我们首先使用 (1 << bitPos) - 1 构造除了当前 tick 以外右侧均为 1 的掩码,然后使用 + (1 << bitPos) 的方法将当前 tick 也置为 1。所以上述代码是可以检索到当前 tick 自身的。关于为什么允许该函数返回当前 tick,读者可以在后文知晓原因。
然后,将 mask 与存储内的位图做 and 操作即可提取获得 masked。最后,我们根据当前区间内是否可以找到此 tick 进行返回。假如当前位图内存在,那么就使用 next tick = tick - bit pos + next bit pos 方法计算,即 (compressed - int24(bitPos - BitMath.mostSignificantBit(masked))) * tickSpacing。而假如当前位图不存在,那么使用 (compressed - int24(bitPos)) * tickSpacing ,此方法等同于直接直接返回当前位图最左侧的索引以方便下一步检索。
接下来,我们分析如果寻找比当前 tick 更大的下一个被初始化的 tick,流程图如下图:
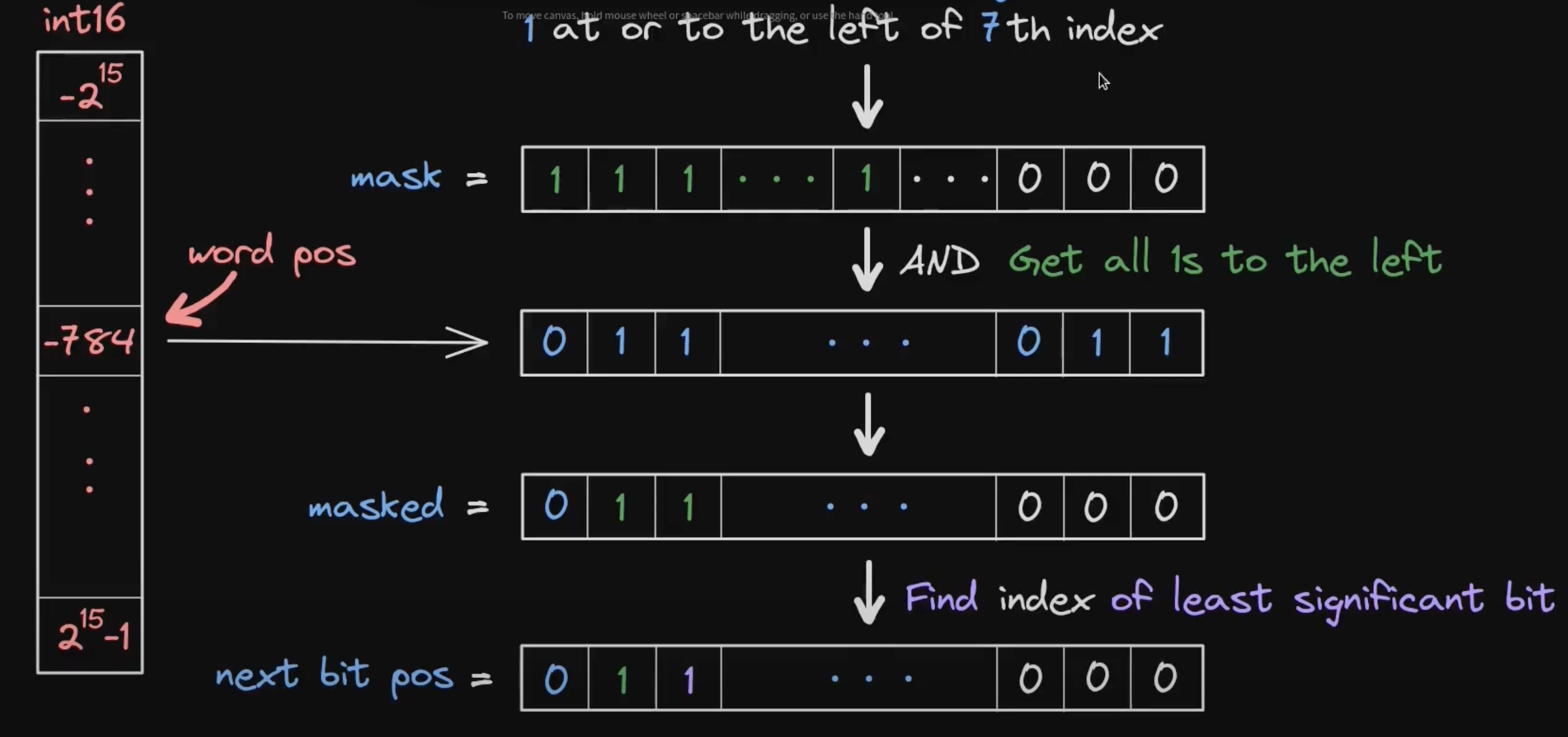
此处的 Find index of least significant bit 是寻找当前位图内最小的位元,该位元也是当前 tick 最近的左侧位元。注意,此处我们会发现由于寻找的 masked 内最小的位元,所以我们不能在最终产生的 masked 内包含当前 tick。具体来说在生成 mask 时,我们就需要去掉当前 tick。所以我们可以使用以下算法计算距离当前 tick 最新的左侧 tick 的位置,此处的 bit pos 实际上是 tick + 1 的 bit pos:
next tick = (tick + 1) - bit pos(tick + 1) + next bit pos
此部分代码需要在 nextInitializedTickWithinOneWord 的 else 分支内进行实现。具体代码如下:
(int16 wordPos, uint8 bitPos) = position(compressed + 1);
uint256 mask = ~((1 << bitPos) - 1);
uint256 masked = self[wordPos] & mask;
initialized = masked != 0;
next = initialized
? (compressed + 1 + int24(uint24(BitMath.leastSignificantBit(masked) - bitPos))) * tickSpacing
: (compressed + 1 + int24(uint24(type(uint8).max - bitPos))) * tickSpacing;
此处我们先获得了 position(compressed + 1) 的位置。正如上文所述,在求解距离当前 tick 最近的右侧 tick 时,我们需要排除掉当前 tick 的影响,所以此处使用了 position(compressed + 1) 进行相关计算。最后求解 next 时也使用了 compressed + 1 。假如没有在当前区间找到合适的 tick,那么会将 next 置为当前 word 的最大值。
我们已经完成了 TickBitmap 库的构建,我们将其导入到主合约内进行一些其他工作。在 _updatePosition 函数内,我们之前定义了 flippedLower 和 flippedUpper 用来表示 tick 是否会被翻转。但我们之前并没有完成此工作。在上文内,我们已经构造了 flipTick 函数,我们可以直接在此处使用:
if (flippedLower) {
tickBitmap.flipTick(tickLower, tickSpacing);
}
if (flippedUpper) {
tickBitmap.flipTick(tickUpper, tickSpacing);
}
上述代码还有一个特殊作用,由于我们在 flipTick 内进行了 tickSpacing 的校验,所以此处当用户不按照 tickSpacing 添加流动性时会出现报错。
在上文介绍 swap 时,我们并没有完成 tickNext 的真正检索。由于我们此处已经实现了 nextInitializedTickWithinOneWord 函数,所以此处也可以引入真实函数进行操作。在 swap 函数内部,我们可以增加以下代码:
(step.tickNext, step.initialized) =
tickBitmap.nextInitializedTickWithinOneWord(state.tick, tickSpacing, zeroForOne);
此处最为麻烦的就是 nextInitializedTickWithinOneWord 中的 lte 参数,当该参数为 true 时,意味着向左寻找 tick,即向较小价格搜索。而在上文内,我们已经推导过 zeroForOne 实际上就是向较小价格移动,所以此处我们直接将 zeroForOne 置为 lte 参数。
这里涉及一个非常有意思的问题,在循环内,每次调用 nextInitializedTickWithinOneWord 都会进行搜索,而且如果当前调用没有获得合适的 tick,那么下一次调用会进入下一个 word 进行检索。在具体机制实现内,对于 lte = true 的情况,我们会在核心的循环最后,使用了 step.tickNext - 1 直接将 step.tickNext 向下移动,手动进入下一个 word 进行搜索。
而当 lte = false 时,假如第一次没有搜索到合适的 tick,那么 step.tickNext 会被置为当前 word 的最大值,当第二次调用此函数时,我们可以看到 (int16 wordPos, uint8 bitPos) = position(compressed + 1); 代码,直接将当前 tick 通过加 1 的方法推入了下一个 word 区间。
完成 Swap 核心
在上文内,我们已经为 swap 积累了大量代码。接下来,我们将再次补齐 swap 所需要的库函数。一个用于跨越 tick 的函数。该函数将在 clamm/src/libraries/Tick.sol 内实现,其实现如下:
function cross(
mapping(int24 => Tick.Info) storage self,
int24 tick,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128
) internal returns (int128 liquidityNet) {
Tick.Info storage info = self[tick];
info.feeGrowthOutside0X128 = feeGrowthGlobal0X128 - info.feeGrowthOutside0X128;
info.feeGrowthOutside1X128 = feeGrowthGlobal1X128 - info.feeGrowthOutside1X128;
liquidityNet = info.liquidityNet;
}
该函数实际上用于当 swap 穿过 tick 时,该函数用于返回 liquidityNet 来调整当前可用于 swap 的流动性数量。除此外,还有一部分功能用于手续费计算,我们会在后文介绍手续费计算部分时再次介绍此处的代码。
我们需要在跨越含有流动性的 tick 时触发此函数。我们可以使用以下方法:
if (state.sqrtPriceX96 == step.sqrtPriceNextX96) {
if (step.initialized) {
int128 liquidityNet = tick.cross(
step.tickNext,
(zeroForOne ? state.feeGrowthGlobalX128 : feeGrowthGlobal0X128),
(zeroForOne ? feeGrowthGlobal1X128 : state.feeGrowthGlobalX128)
);
if (zeroForOne) liquidityNet = -liquidityNet;
state.liquidity = liquidityNet < 0
? state.liquidity - uint128(-liquidityNet)
: state.liquidity + uint128(liquidityNet);
}
state.tick = zeroForOne ? step.tickNext - 1 : step.tickNext;
}
此处我们使用 state.sqrtPriceX96 == step.sqrtPriceNextX96 判断当前 swap 后是否到达了价格区间边界,但是到达价格区间边界不意味着需要调整流动性,因为有可能穿过了一个没有流动性的价格区间。我们可以通过 step.initialized 判断刚刚穿过的价格区间是否具有流动性。假如 step.initialized = true 说明穿过一个有效的价格区间,我们需要进行流动性调整和手续费更新。在调用 tick.cross 函数时,最为复杂的就是 feeGrowthGlobal0X128 和 feeGrowthGlobal1X128 的参数问题。具体情况如下:
- 当
zeroForOne = true时,我们对 token 0 征收手续费,所以feeGrowthGlobal0X128参数部分传入了state.feeGrowthGlobalX128以方便cross函数使用最新的feeGrowthGlobal0X128更新,而feeGrowthGlobal1X128参数部分则传入了feeGrowthGlobal1X128,因为此部分直接读取存储即可,不需要使用内存内的最新数据 - 当
zeroForOne = false时,我们对token 1征收手续费,所以feeGrowthGlobal1X128参数部分传入了位于内存中的最新的state.feeGrowthGlobalX128,而feeGrowthGlobal0X128部分则不需要使用最新数据
在上述 crossTick 被调用的代码最后,我们完成了 state.liquidity 的更新,此处需要注意如果用户使用 zeroForOne ,意味着我们每次都是从区间上限进入,从区间下限退出,这与 liquidityNet 的预设条件(从下限进入,从上限退出) 相反,所以此处编写了 if (zeroForOne) liquidityNet = -liquidityNet; 代码来应对此情况。
最后,为了保证每次下一次循环可以进入下一个 word 区间,所以此处使用了 state.tick = zeroForOne ? step.tickNext - 1 : step.tickNext; 来更新 step.tickNext 变量。这导致如果使用 zeroForOne 模式,后续传入的 tick 实际上是上一次 tick 减去 1,手动将 tick 推入下一个 word 以方便检索。
最后,我们讨论一下 state.sqrtPriceX96 != step.sqrtPriceNextX96 的情况,这说明 swap 没有耗尽当前区间的流动性,这其实也意味着 swap 的结束。在这种情况下,我们需要计算最新的 tick 来保证后续的存储写入环节。
if (state.sqrtPriceX96 == step.sqrtPriceNextX96) {
if (step.initialized) {
int128 liquidityNet = ticks.cross(
step.tickNext,
(zeroForOne ? state.feeGrowthGlobalX128 : feeGrowthGlobal0X128),
(zeroForOne ? feeGrowthGlobal1X128 : state.feeGrowthGlobalX128)
);
if (zeroForOne) liquidityNet = -liquidityNet;
state.liquidity = liquidityNet < 0
? state.liquidity - uint128(-liquidityNet)
: state.liquidity + uint128(liquidityNet);
}
state.tick = zeroForOne ? step.tickNext - 1 : step.tickNext;
} else if (state.sqrtPriceX96 != step.sqrtPriceStartX96) {
state.tick = TickMath.getTickAtSqrtRatio(state.sqrtPriceX96);
}
至此,我们完成了 swap 内部除手续费计算以外的几乎全部逻辑。
手续费计算
在 Uniswap V3 内部,每一个 tick 只能获得 tick 内部的手续费。我们定义 Uniswap V3 池子收取的全部手续费为 $f_g$,注意此手续费与 tick 无关,指所有 tick 收取的手续费之和。然后,我们定义发生在 tick 流动性区间左侧的交易所获得手续费为 $f_b$,发生在 tick 右侧的交易所获得的手续费为 $f_a$。我们可以推导价格区间 $[i_L, i_U]$ 内, $f(i_L, i_U) = f_g - f_b(i_L) - f_a(i_U)$。使用该公式可以非常简单的计算出当前区间的手续费。对于参数 $f_g$ ,该参数代表全局的手续费收入,我们可以非常简单的计算。但时我们面前不知道如何正确求解出 $f_b(i_L)$ 和 $ f_a(i_U)$ 参数。为了求解这些参数,我们引入 $f_o(i)$ 的定义,该定义指当前 tick i 在当前价格对侧积累的手续费数量,如下图:
当 tick i 大于当前价格时,$f_o(i)$ 指
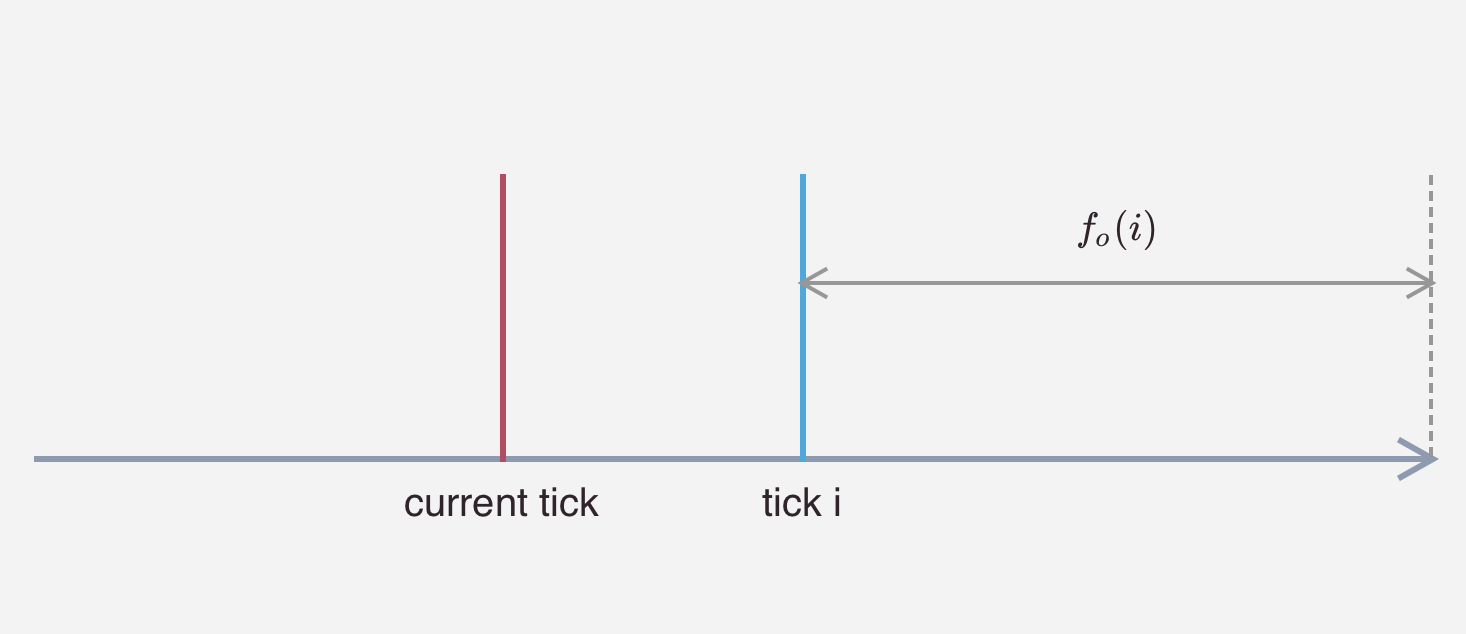
当 tick i 小于当前价格时,$f_o(i)$ 指:
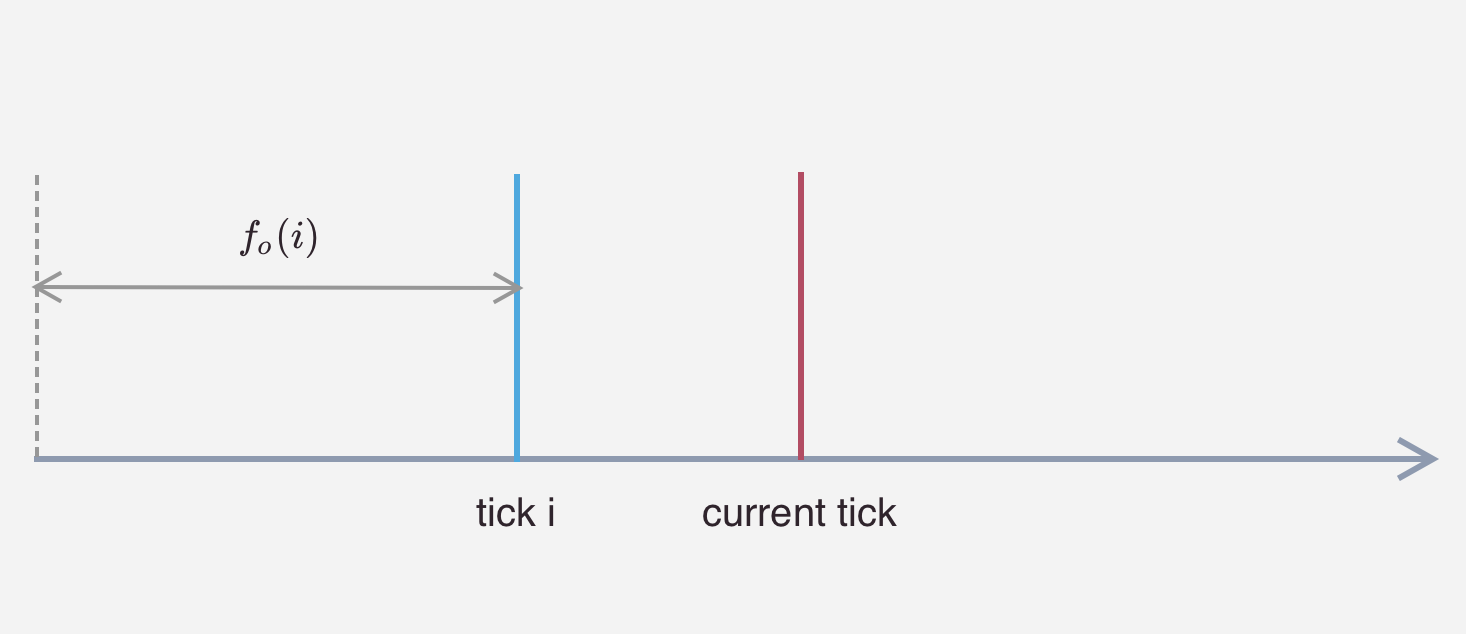
基于上述定义,我们可以获得如下结论: $$ f_a(i) = \begin{cases} f_g - f_o(i) &i_c \geq i \\ f_o(i) & i_c < i \end{cases} $$ 也可以获得如下结论: $$ f_b(i) = \begin{cases} f_o(i) &i_c \geq i \\ f_g - f_o(i) & i_c < i \end{cases} $$ 另外,我们也发现当 current tick 穿过当前的 tick i 时,我们需要使用 $f^{new}_o(i) = f_g - f_o(i)$ 更新当前的 $f_o(i)$ 的数值。
结合上文给出的 $f(i_L, i_U) = f_g - f_b(i_L) - f_a(i_U)$ 的计算公式,我们可以获得如下结果: $$ f(i_L, i_U) = \begin{cases} f_o(b) - f_o(a) & i_c < i_L < i_U \\ f_g - f_o(a) - f_o(b) & i_L < i_c < i_U \\ f_o(a) - f_o(b) & i_L < i_U < i_c \end{cases} $$ 但是我们在初始化 $f_o(i)$ 时很难计算出一侧的手续费数值。可以想象由于 $f_o(i)$ 代表当前价格对侧的手续费,该数值是很难直接计算的,至少没办法只使用 $f_g$ 计算获得。所以我们尝试使用一个错误的 $f_o’(i)$ 进行计算。
但此处我们使用增量进行计算,因为我们实际上只关心某一个流动性区间相对于上次创建时的手续费收入。我们定义变量 $last$ ,该变量代表在区间创建时使用错误的 $f’_o(i)$ 计算的手续费数值。由于我们计算的是手续费增量,所以存在以下公式: $$ \Delta fee = now - last $$ 此处的 $fee$ 就是指在某一段时间内积累的手续费数量。注意,我们在上文说使用一个错误的 $f’(o)$ 进行计算,所以我们不确定是否可以计算出正确的结果。接下来,我们进行分类讨论几种情况以确认创建区间时使用任何 $f’(o)$ 都是合理的。
第一种情况时,创建区间时 $i_c < i_L < i_U$ ,即创建区间时的价格低于当前的流动性区间,而经过一段时间后,价格仍未移动到流动性区间内部,保持 $i_c < i_L < i_U$,此时存在: $$ \begin{align} init &= f’_o(b) - f’_o(a) \\ now &= f’_o(b) - f’_o(a) \\ \Delta fee &= 0 \end{align} $$ 上述情况计算出的结果是正确的。因为价格始终没有移动到流动性区间内部,所以流动性区间获得的手续费应该是 0。事实上,初始化时为 $i_L < i_U < i_c$,计算手续费时价格为 $i_L < i_U < i_c$,上述结论也是成立的。
第二种情况时,创建区间时 $i_c < i_L < i_U$ ,但经过一段时间后,价格向右移动到价格区间内部,即 $i_L < i_c < i_U$。如下图所示:
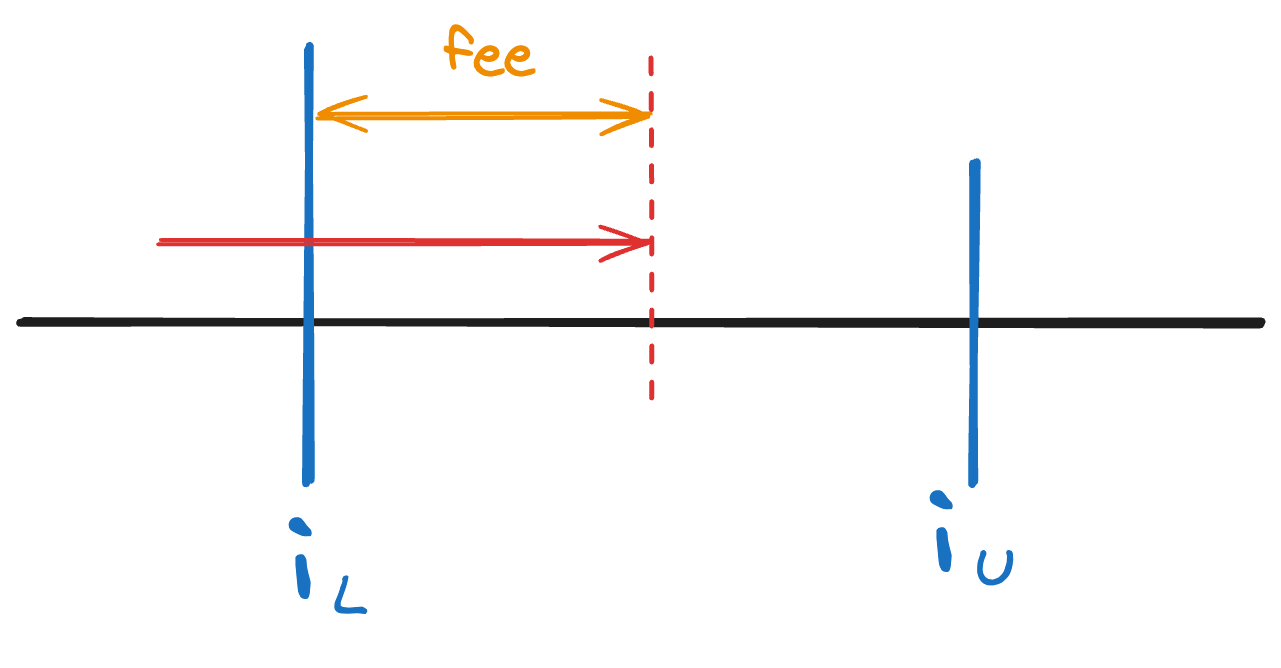
根据我们的公式可以计算获得: $$ \begin{align} init &= f'_o(b) - f'_o(a) \\ f''_o(b) &= f_g' - f'_o(b) &\text{when } i_c = i_L \\ now &= f_g'' - f'_o(a) -f''_o(b) \\ \Delta fee &= f_g' - f''_o(b) - f'_o(b) \\ &= f_g'' - f_g' \end{align} $$ 此处的 $f’_g$ 实际上记录了在价格进入当前价格区间时的全局手续费数量,而 $f_g’’$ 指计算时的全局手续费数量,显然,当 $f_g’’ - f_g’$ 时,计算结果是正确的。
第三种情况,初始化时价格为 $i_c < i_L < i_U$,但计算手续费时 $i_L < i_U < i_c$,我们可以获得以下结论: $$ \begin{align} init &= f'_o(b) - f'_o(a) \\ f''_o(b) &= f_g' - f'_o(b) &\text{when } i_c = i_L \\ f''_o(a) &= f_g''' - f'_o(a) &\text{when } i_c = i_U \\ now &= f''_o(a) - f''_o(b) \\ \Delta fee &= f''_o(a) - f''_o(b) - init \\ &= f_g''' - f_g' \end{align} $$ 此处的 $f’_g$ 实际上记录了在价格进入当前价格区间时的全局手续费数量,而 $f_g’’’$ 指价格离开区间时的全局手续费数量,此处的计算结果也是正确的。读者可以自行验证任何的价格移动情况,或者多次穿过价格区间上限和下限的移动情况,最终都会得到一个与 $f_o(i)$ ,且只与不同时间的 $f_g$ 有关的结果。所以我们实际上可以将 tick i 初始化为任意数值。但在 Uniswap 内,Uniswap 的开发者约定: $$ f_o(i) = \begin{cases} f_g &i_c \geq i \\ 0 & i_c < i \end{cases} $$
上述讨论只是为了让读者理解为什么我们可以随意初始化 tick。但在实际编码时,我们只需要以下两个公式:
$$
f(i_L, i_U) = \begin{cases}
f_o(b) - f_o(a) & i_c < i_L < i_U\\
f_g - f_o(a) - f_o(b) & i_L < i_c < i_U\\
f_o(a) - f_o(b) & i_L < i_U < i_c
\end{cases}
$$
以及
$$
f^{new}_o(i) := f_g - f_o(i)
$$
我们首先将初始化完成,在 clamm/src/libraries/Tick.sol 内,我们会使用 update 函数实现初始化:
if (liuquidityGrossBefore == 0) {
if (tick <= tickCurrent) {
info.feeGrowthOutside0X128 = feeGrowthGlobal0X128;
info.feeGrowthOutside1X128 = feeGrowthGlobal1X128;
}
info.initialized = true;
}
当我们发现 tick <= tickCurrent 成立时,此时 $f_o(i)$ 应该被初始化为 $f_g$ ,即此处的 feeGrowthGlobal0X128 和 feeGrowthGlobal1X128。而当 tick > tickCurrent 时,我们不需要初始化,参数会被默认置为 0。
根据我们在上文的介绍,我们还需要计算 $f(i_L, i_U)$ 。在 clamm/src/libraries/Tick.sol 内,我们实现 getFeeGrowthInside 函数:
function getFeeGrowthInside(
mapping(int24 => Tick.Info) storage self,
int24 tickLower,
int24 tickUpper,
int24 tickCurrent,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128
) internal view returns (uint256 feeGrowthInside0X128, uint256 feeGrowthInside1X128) {
Info storage lower = self[tickLower];
Info storage upper = self[tickUpper];
unchecked {
uint256 feeGrowthBelow0X128;
uint256 feeGrowthBelow1X128;
if (tickCurrent >= tickLower) {
feeGrowthBelow0X128 = lower.feeGrowthOutside0X128;
feeGrowthBelow1X128 = lower.feeGrowthOutside1X128;
} else {
feeGrowthBelow0X128 = feeGrowthGlobal0X128 - lower.feeGrowthOutside0X128;
feeGrowthBelow1X128 = feeGrowthGlobal1X128 - lower.feeGrowthOutside1X128;
}
uint256 feeGrowthAbove0X128;
uint256 feeGrowthAbove1X128;
if (tickCurrent < tickUpper) {
feeGrowthAbove0X128 = upper.feeGrowthOutside0X128;
feeGrowthAbove1X128 = upper.feeGrowthOutside1X128;
} else {
feeGrowthAbove0X128 = feeGrowthGlobal0X128 - upper.feeGrowthOutside0X128;
feeGrowthAbove1X128 = feeGrowthGlobal1X128 - upper.feeGrowthOutside1X128;
}
feeGrowthInside0X128 = feeGrowthGlobal0X128 - feeGrowthBelow0X128 - feeGrowthAbove0X128;
feeGrowthInside1X128 = feeGrowthGlobal1X128 - feeGrowthBelow1X128 - feeGrowthAbove1X128;
}
}
上述代码依次计算了 $f_a$ 和 $f_b$ ,并使用 $fee = f_g - f_a - f_b$ 计算了当前的手续费情况,此处由于我们在池子内存在两种代币,所以此处需要依次计算每一种代币的数额。值得注意的是,此处我们使用了 unchecked 代码块,是因为即使 uint256 计算溢出也可以获得正确的手续费结果。这部分实际上与 uint256 溢出计算的性质有关,即使出现了溢出计算,我们最终由于结果并不以依赖于 $f_o(a)$ 和 $f_o(b)$ ,所以溢出计算并不会产生影响。读者也可以尝试在数学上进行证明。
最后,我们实现 $f^{new}_o(i) := f_g - f_o(i)$ 公式,其实就是我们在前文内实现的 cross 函数,但我们在此处会修复一个之前编写时留下的小错误:
function cross(
mapping(int24 => Tick.Info) storage self,
int24 tick,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128
) internal returns (int128 liquidityNet) {
Tick.Info storage info = self[tick];
unchecked {
info.feeGrowthOutside0X128 = feeGrowthGlobal0X128 - info.feeGrowthOutside0X128;
info.feeGrowthOutside1X128 = feeGrowthGlobal1X128 - info.feeGrowthOutside1X128;
}
liquidityNet = info.liquidityNet;
}
此处使用 unchecked 原因还是因为溢出计算并不会影响手续费计算的最终结果。
至此我们修复了 tick 内部的更新逻辑。接下来,我们需要完成 position 内部的手续费逻辑更新部分。
我们在 clamm/src/libraries/Position.sol 内的 update 函数内部实现手续费的计算逻辑:
uint128 tokensOwed0 = uint128(
FullMath.mulDiv(feeGrowthInside0X128 - _self.feeGrowthInside0LastX128, _self.liquidity, FixedPoint128.Q128)
);
uint128 tokensOwed1 = uint128(
FullMath.mulDiv(feeGrowthInside1X128 - _self.feeGrowthInside1LastX128, _self.liquidity, FixedPoint128.Q128)
);
此处我们需要注意 feeGrowthInside0X128 和 feeGrowthInside1X128 实际上都是记录的单位流动性可获得的手续费数量,而此处我们使用 fee * liquidity 的公式计算用户提供的流动性可获得的手续费数量,但是该数量的精度是存在问题的,因为 fee 使用了 $2^{128}$ 精度,所以最终直接计算出的结果需要除以 $2^{128}$。这也是上述代码使用了 FullMath.mulDiv 的原因。最后我们在 update 函数将计算获得的手续费增加到用户可提取的部分内:
if (tokensOwed0 > 0 || tokensOwed1 > 0) {
self.tokensOwed0 += tokensOwed0;
self.tokensOwed1 += tokensOwed1;
}
至此,我们也完成了 Position 的 update 函数。
接下来,我们需要在 _updatePosition 函数内更新手续费计算逻辑,_updatePosition 用于更新价格区间的数据,我们需要在更新相关数据时增加手续费计算逻辑。为了节省 gas,我们仍需要在内存内之前缓存数据:
uint256 _feeGrowthGlobal0X128 = feeGrowthGlobal0X128;
uint256 _feeGrowthGlobal1X128 = feeGrowthGlobal1X128;
然后,我们在此处使用 ticks.getFeeGrowthInside 计算手续费并将其更新到 Position 内部。
(uint256 feeGrowthInside0X128, uint256 feeGrowthInside1X128) =
ticks.getFeeGrowthInside(tickLower, tickUpper, tick, _feeGrowthGlobal0X128, _feeGrowthGlobal1X128);
position.update(liquidityDelta, feeGrowthInside0X128, feeGrowthInside1X128);
我们在上文有所提及,feeGrowthGlobal0X128 和 feeGrowthGlobal1X128 都是单位流动性可获得的手续费的数量。所以我们需要在 swap 函数内部更新该函数。以下代码位于 swap 的核心循环内部,代码如下:
if (state.liquidity > 0) {
state.feeGrowthGlobalX128 += FullMath.mulDiv(step.feeAmount, FixedPoint128.Q128, state.liquidity);
}
上述代码使用 computeSwapStep 计算获得 step.feeAmount ,然后将 step.feeAmount 的精度通过乘法扩展到 Q128 内部,然后除以当前的流动性情况就可以获得当前单位流动性可获得的手续费数量。
总结
在本文内,我们基本完成了 Uniswap V3 的所有代码分析,但本文没有涉及以下内容:
- Uniswap V3 的协议费用
- 预言机部分
- 数学库的计算
总体来说,Uniswap V3 是一个具有相当复杂性的合约。这些复杂性来自大量的三目表达式使用,以及支持多种交换模式。比如在上文内频繁出现的 zeroForOne 或者 exactIn 等,这些复杂的兑换模式要在同一个函数内兼容是会带来大量三目表达式的。对于手续费计算部分,Uniswap V3 的手续费计算逻辑也是较难理解的。