概述
椭圆曲线密码学是现代区块链的核心之一,Ethereum 和 Bitcoin 等都依赖于椭圆曲线密码学(Elliptic-curve Cryptography,简称为 ECC)。在本文中,我们将介绍 Ethereum 使用的椭圆曲线算法 secp256k1 并尝试从零开始实现它。
本文不仅仅会实现一个基础版本的 secp256k1 并且会进行一系列的优化,使其最终生产可用。事实上,读者可以视本文为 noble-secp256k1 的源代码分析文章。本文的主要内容也参考了 noble-secp256k1 作者 paulmillr 编写的 Learning fast elliptic-curve cryptography 博客。本文另有部分内容参考了 Guide to Elliptic Curve Cryptography ,读者可以相当容易的在网上找到此处的电子版。本文还有部分内容选自 Pairings for beginners。
在阅读本文之前,建议读者阅读 基于链下链上双视角深入解析以太坊签名与验证。本文所有的代码可以从 zero-secp256k1 仓库内获得。
初始化
由于本文是一个实战项目,所以需要读者使用任意 typescript 包管理工具进行项目的创建。并安装 @noble/secp256k1 依赖。笔者偏好使用 bun 直接作为包管理和运行工具。我们可以使用如下命令创建一个新项目:
mkdir zero-secp256k1
cd zero-secp256k1
bun init
完成以上命令后,使用 bun i @noble/secp256k1 安装依赖,我们安装此依赖的原因是对比该库的输出已确定我们编写的代码的正确性。
椭圆域计算
我们首先实现公钥计算,总所周知,椭圆曲线的公钥计算方法如下: $$ Q = G \cdot q $$ 其中,$G$ 为常数而 $q$ 为私钥。而 $G\cdot q = G + G + G + \dots$ ,所以我们只需要实现椭圆曲线上的加法就可以进行公钥计算。但实际上直接累加 $q$ 个 $G$ 的计复杂度比较高,我们希望使用一种方法简化计算复杂度。一个最简单且有效的简化计算复杂度的方案是引入倍增计算,所谓倍增计算,就是已知 $G$ 的情况下,快速计算 $2G$。使用此算法,我们可以把对 $q$ 个 $G$ 的累加简化为 $log_2q$ 的倍增。
下图展示椭圆曲线内的加法和倍增计算(注意,下图显示的并不是 secp256k1 曲线):
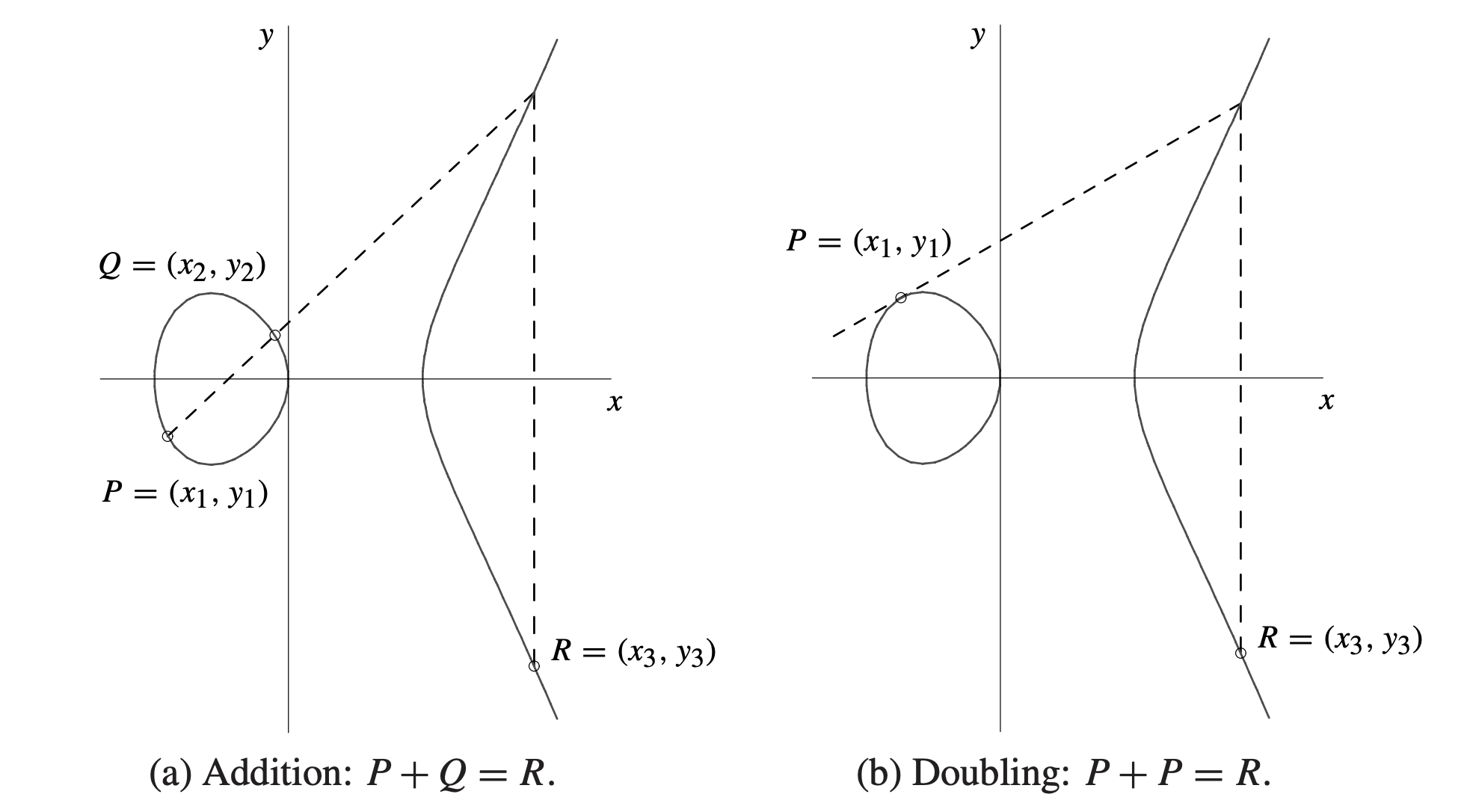
在本文中,我们将不加推导的直接给出相关计算公式。该计算公式来源于 Guide to Elliptic Curve Cryptography。对于任意符合 $y^2=x^3+a*x+b$ 的曲线都可以使用。而 secp256k1 曲线的形式为 $y^2 = x^3 + 7$,下图内的公式都可以直接将 $a = 0$ 代入。
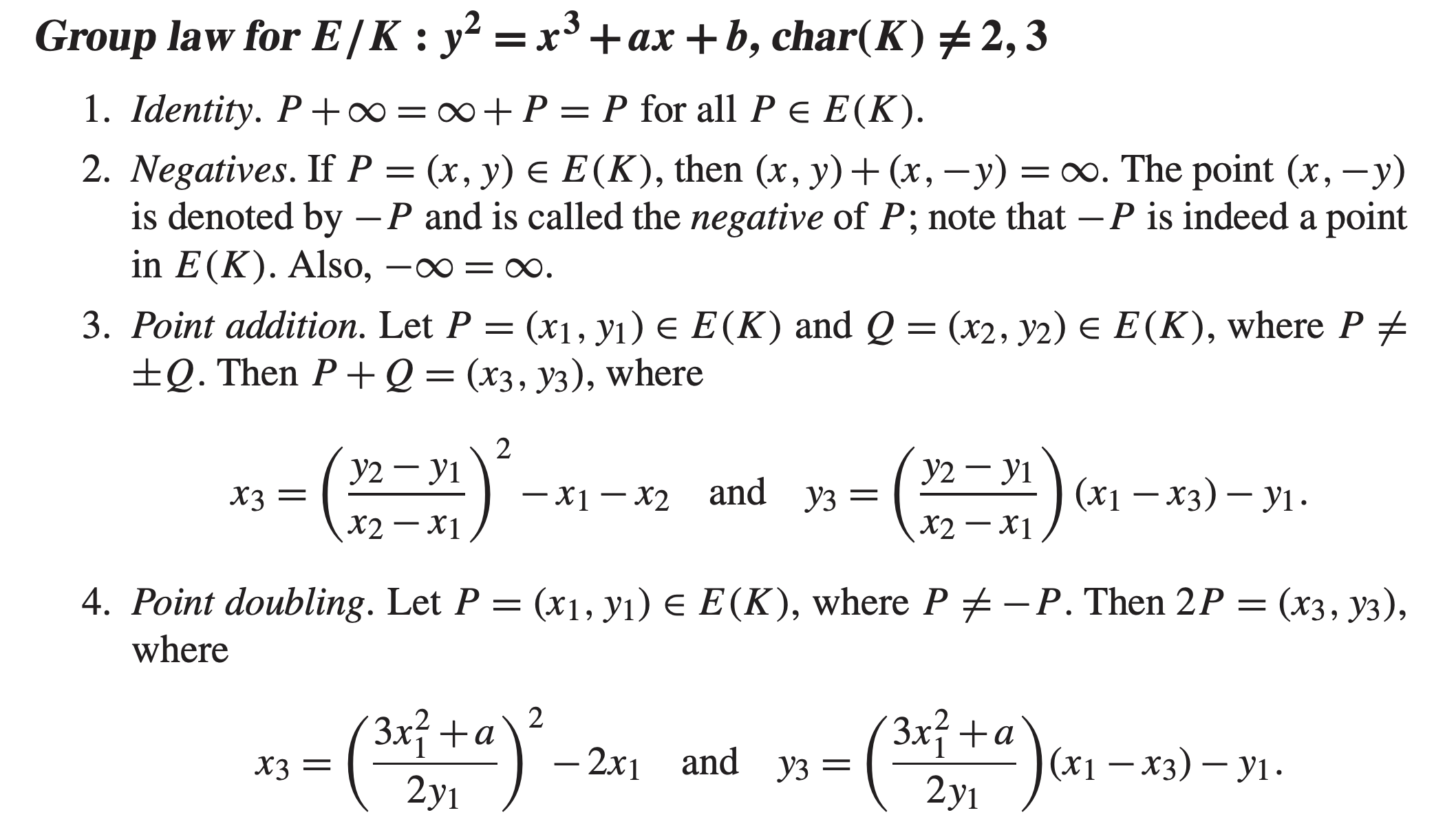
可能部分读者可以在密码学文献内看到 short Weierstrass equation 名词,该名词实际就指 $y^2=x^3+a*x+b$ 形式的椭圆曲线函数
此处需要注意一点,上述所有的计算都需要在有限域 $\mathbb F_P$内的完成,或者更加简单的来说,所有计算的结果都需要模除 $G$。我们举出几个简单的例子,假设如下算法都发生在 $\mathbb F_{29}$ 内:
- 加法:$17+20 = 8$ 因为 $37 \mod 29 = 8$
- 减法:$17−20 = 26$ 因为 $−3 \mod 29 = 26$
- 乘法:$17 \cdot 20 = 21$ 因为 $340 \mod 29 = 21$
- 求逆:$17^{−1} = 12$ 因为 $17 · 12 \mod 29 = 1$
对于如何在有限域内进行求逆计算,我们可以使用拓展欧几里得算法计算。计算原理是扩展欧几里得算法可以计算出 $\gcd(29, 17) = s \cdot 29 + t \cdot 17$ 中的 $s$ 和 $t$。补充一个数论知识,任何可以求出逆元的整数,其与模数(在此案例中为 $29$)的最大公因子是 $1$。在此前提下,那么 $1 = s \cdot 29 + t \cdot 17$,两侧同时模除 $29$,即获得 $t \cdot 17 \mod 29 = 1$。经过如上推导,不难看出计算逆元的方法是使用扩展欧几里得算法,直接计算 $t$ 即可。
扩展欧几里得算法的伪代码如下:

综合上述知识,我们已经知道了如何在 $\mathbb F_G$ 有限域内进行加减乘除计算,所谓除法只需要乘以逆元即可。同时,我们也拿到了椭圆曲线上的倍增和加法算法,由此,我们就可以直接实现 $Q = G \cdot p$ 算法,并最终实现私钥推导公钥的算法。
我们首先实现最为简单的扩展欧几里得算法求解逆元:
const CURVE = {
P: 2n ** 256n - 2n ** 32n - 977n,
n: 2n ** 256n - 432420386565659656852420866394968145599n,
};
const mod = (a: bigint, b: bigint = CURVE.P): bigint => {
const result = a % b;
return result >= 0 ? result : b + result;
};
const invert = (number: bigint, modulo: bigint = CURVE.P): bigint => {
if (number === 0n || modulo <= 0n) {
throw new Error(
`invert: expected positive integers, got n=${number} mod=${modulo}`,
);
}
let a = mod(number, modulo);
let b = modulo;
let x = 0n,
y = 1n,
u = 1n,
v = 0n;
while (a !== 0n) {
const q = b / a;
const r = b % a;
const m = x - u * q;
const n = y - v * q;
b = a;
a = r;
x = u;
y = v;
u = m;
v = n;
}
const gcd = b;
if (gcd !== 1n) throw new Error("invert: does not exist");
return mod(x, modulo);
};
在此处,我们也引入了 secp256k1 曲线的一些基本信息,此处的 CURVE.P 就是有限域的大小,而 CURVE.n 则是另一个参数。这些参数对程序员而言无法背后的密码学原理,我们可以直接照抄即可。在 SEC 2: Recommended Elliptic Curve Domain Parameters 可以获得这些参数。更加现代的方法是使用 Standard curve database 网站,可以在 SECG 目录内找到 secp256k1 曲线。

这里的 $G$ 使用了一种编码方法将 $(x, y)$ 使用十六进制表示,读者可以自行参考 此文档 了解
完成上述代码后,我们可以创建一个基础的测试来判断我们的代码是否正确。我们使用 $\mathbb F_{29}$ 的例子进行测试:
import { expect, test, describe } from "bun:test";
import { invert, mod } from "..";
describe("f29 fields arithmetic", () => {
test("17 + 20", () => {
expect(mod(17n + 20n, 29n)).toBe(8n);
});
test("17 − 20", () => {
expect(mod(17n - 20n, 29n)).toBe(26n);
});
test("17 * 20", () => {
expect(mod(17n * 20n, 29n)).toBe(21n);
});
test("17^(-1)", () => {
expect(invert(17n, 29n)).toBe(12n);
});
});
完成以上有限域的代码后,我们可以真正实现椭圆域上的计算:
export class Point {
static ZERO = new Point(0n, 0n);
constructor(
public x: bigint,
public y: bigint,
) {}
double(): Point {
const X1 = this.x;
const Y1 = this.y;
const lam = mod(3n * X1 ** 2n * invert(2n * Y1, CURVE.P));
const X3 = mod(lam * lam - 2n * X1);
const Y3 = mod(lam * (X1 - X3) - Y1);
return new Point(X3, Y3);
}
add(other: Point): Point {
const [a, b] = [this, other];
const [X1, Y1, X2, Y2] = [a.x, a.y, b.x, b.y];
if (X1 === 0n || Y1 === 0n) return b;
if (X2 === 0n || Y2 === 0n) return a;
if (X1 === X2 && Y1 === Y2) return this.double();
if (X1 === X2 && Y1 === -Y2) return Point.ZERO;
const lam = mod((Y2 - Y1) * invert(X2 - X1, CURVE.P));
const X3 = mod(lam * lam - X1 - X2);
const Y3 = mod(lam * (X1 - X3) - Y1);
return new Point(X3, Y3);
}
}
以上计算都较为简单,相信读者也可以自行根据公式实现。此处的 add 函数增加了部分条件判断语句,其目的是简化一些不必要的计算。
最后,我们完成一个较为复杂的任务,即公钥计算。正如前文所述,计算公钥只需要将 $p$ 个 $G$ 相加。我们可以使用倍增算法优化时间复杂度。我们首先将 $G$ 点的配置写入 CURVE:
const CURVE = {
P: 2n ** 256n - 2n ** 32n - 977n,
n: 2n ** 256n - 432420386565659656852420866394968145599n,
Gx: 55066263022277343669578718895168534326250603453777594175500187360389116729240n,
Gy: 32670510020758816978083085130507043184471273380659243275938904335757337482424n,
};
之后,我们可以在 Point 类型内加入以下方法:
multiplyDA(n: bigint): Point {
let p = Point.ZERO;
let d: Point = this;
while (n > 0n) {
if (n & 1n) p = p.add(d);
d = d.double();
n >>= 1n;
}
return p;
}
以上代码简单来说就是当 n 是奇数时,执行 n / 2 次倍增,然后执行一次加法,而当 n 是偶数时,执行 n / 2 次倍增,而不执行加法操作。
完成以上算法后,我们就可以进行一次简单的测试,测试我们是否可以根据私钥计算出公钥。
import { expect, test, describe } from "bun:test";
import { utils, getPublicKey, ProjectivePoint } from "@noble/secp256k1";
import { Point, CURVE } from "..";
describe("public key", () => {
test("random private key", () => {
const privKey = utils.randomPrivateKey();
const secp256k1Point = ProjectivePoint.fromPrivateKey(privKey);
const G = new Point(CURVE.Gx, CURVE.Gy);
const pubKeyPoint = G.multiplyDA(utils.normPrivateKeyToScalar(privKey));
expect(pubKeyPoint.x).toBe(secp256k1Point.x);
expect(pubKeyPoint.y).toBe(secp256k1Point.y);
});
});
在此处,我们引入了 @noble/secp256k1 内的部分函数来进行相等性测试,测试结果说明,我们编写的 multiplyDA 函数已经可以完成基础的私钥对公钥的计算。
计时攻击
上述编写的代码存在一个严重的漏洞,即上述代码可以被计时攻击。所谓计时攻击是一种常见的侧信道攻击方案,假如我们存在一个为用户签名的程序,黑客可以调用该程序,但并不知道程序的私钥。此时黑客可以尝试使用该程序签名大小不同的数据,并根据签名的时间推测程序的私钥。为了规避计时攻击,我们的方案往往是实现一个对任意输入都会以相同时间处理的程序。
为了更加清楚的获得函数的执行效率,我们需要使用 bun add mitata 安装性能测试框架,该框架可以检测代码的执行效率。我们可以编写一下性能测试代码:
import { bench, run } from "mitata";
import { Point, CURVE } from "..";
bench("small", () => {
const G = new Point(CURVE.Gx, CURVE.Gy);
G.multiplyDA(2n);
});
bench("big", () => {
const G = new Point(CURVE.Gx, CURVE.Gy);
G.multiplyDA(2n ** 255n - 19n);
});
await run();
最终的执行结果如下:
clk: ~3.91 GHz
cpu: Apple M3 Max
runtime: bun 1.1.16 (arm64-darwin)
benchmark avg (min … max) p75 p99 (min … top 1%)
------------------------------------------- -------------------------------
small 48.65 µs/iter 50.13 µs ▃█
(39.13 µs … 436.58 µs) 74.38 µs ▆███▆███▅▃▂▁▁▁▁▁▁▁▁▁▁
big 12.86 ms/iter 13.36 ms █ ▂
(11.76 ms … 14.47 ms) 14.37 ms ▇█▇▃▁▅█▅▁▇█▃▅▁▇▃▁▁▇▅▅
可见当前我们编写的代码具有较大可能被计时攻击。我们需要修改代码以避免此情况。一个最为简单修改方案如下:
multiplyDA(n: bigint): Point {
let p = Point.ZERO,
f = Point.ZERO;
let d: Point = this;
for (let i = 0; i <= 256; i++) {
if (n & 1n) p = p.add(d);
else f = f.add(d);
d = d.double();
n >>= 1n;
}
return p;
其原理在于既然较小的数字可能导致较快跳出 while 循环而导致出现计算过快的问题,那么我们通过使用 for 循环强制使得所有私钥的计算都必须进行 256 次。如此就规避了计时攻击的问题。修改后的代码进行性能测试结果如下:
benchmark avg (min … max) p75 p99 (min … top 1%)
------------------------------------------- -------------------------------
small 13.32 ms/iter 13.92 ms ▅ ▂█▅▂ ▂ ▅
(11.86 ms … 14.43 ms) 14.39 ms ▇▁▄▁█▁▄▇▄████▇▇▇█▇█▄▇
big 13.11 ms/iter 13.76 ms ▄ ▄ █ ▄▄ ▄▄ █
(11.79 ms … 14.41 ms) 14.37 ms ██████▅█▅▅██▁███▅▅███
预计算优化
在上文中,我们并没有对 multiplyDA 方法进行优化,在本节中,我们将尝试进行第一次优化,使用 w-ary non-adjacent form (wNAF) method 优化加法方案。
在了解具体的算法内容前,我们首先需要引入一个概念 Non-adjacent form(缩写为 NAF)。这个概念指我们可以将一个任意的正整数 $k$,我们都可以将其转化为 $k = \sum_{i=0}^{l-1}k_i2^i$,其中 $k_i \in {0, 1, -1}$ 且 $k_{l-1} \neq 0$。除了上述限制外,NAF 要求不存在连续的非零 $k_i$ 。
假如存在以下几个表示形式,读者可以根据上述定义判断哪些满足 $k = 7$ 的 NAF 形式:
- 0 1 1 1
- 1 0 -1 1
- 1 −1 1 1
- 1 0 0 −1
上述几个写法中,只有 4 满足 NAF 的所有定义。其中 2 和 3 都是因为存在连续的非零整数而不满足 NAF 的定义。NAF 具有一些有趣的数学属性。其最重要的属性是相比于其他二进制表示,NAF 具有最少的非零位。在计算椭圆曲线域上的乘法时,我们可以快速执行加法和减法操作。而相比于一般的二进制表示,NAF 引入了 -1 使得非零位降低,这使得我们计算乘法时所需要的算力减少。
因为我们可以将 $G$ 转化为 NAF 形式进行计算。我们不加推导的给出以下结论:
- 在使用常规的二进制表示的情况下,计算椭圆曲线上的 $m$ 与 $G$ 相乘,我们需要计算 $\frac{m}{2}A + mD$ 次计算。其中 $A$ 代表加法而 $D$ 代表倍增
- 在使用 NAF 表示的情况下,我们只需要 $\frac{m}{3}A + mD$ 次计算
我们首先实现最简单的 naf 算法,具体算法的论文表述如下:

我们可以快速将上述伪代码转化为 typescript 代码,如下:
export const naf = (number: bigint): bigint[] => {
let k = number;
let result: bigint[] = [];
while (k >= 1) {
let ki: bigint;
if (k & 1n) {
ki = 2n - mod(k, 4n);
k -= ki;
} else {
ki = 0n;
}
k = k / 2n;
result.push(ki);
}
return result.reverse();
};
然后编写如下测试:
describe("naf", () => {
test("naf(7) = 1 0 0 −1", () => {
expect(naf(7n)).toEqual([1n, 0n, 0n, -1n]);
});
});
但是,除了上述简单的 NAF 形式外,我们还有一些更加复杂但更加节省运算的 NAF 形式。我们称之为 width-w NAF。这种形式的 NAF 与上文描述的 NAF 大致相同,但也有其特殊之处。
我们首先给出 width-w NAF 的定义。这个概念与 NAF 的概念高度类似。具体如下:
存在一个任意的正整数 $k$,我们都可以将其转化为 $k = \sum_{i=0}^{l-1}k_i2^i$,其中每一个位于奇数位元的 $k_i$ 都是非零的,且 $|k_i| < 2^{w-1}$, $k_{l-1} \neq 0$。且任意 $w$ 个位元中至多有一个非零。我们一般使用 $\text{NAF}_w(k)$ 表示 $k$ 的 width-w NAF。特殊的,$\text{NAF}_2(k)$ 实际上就是上文中我们描述的 NAF 的定义。

上图内给出了不同宽度的 NAF 的定义。引入 width-w NAF 之后,我们可以使用此概念与预计算实现更加高效的计算。比如我们使用 $\text{NAF}_4(k)$ 进行相关计算。我们可以提前计算出 $P_i = i \cdot G$,其中 $i \in {1, 3, 5,\dots,2^{w-1}-1}$。更加具体的算法如下:

在此处,我们没有具体列出一些相关代码,因为本文参考的 noble-secp256k1 并没有完全使用上述算法,而是使用了一种变体算法。为了简化篇幅,本文不再给出上述完全基于 width-w NAF 的点的乘法算法实现。
我们首先考虑如何生成一个类似 width-w NAF 形式的数组。我们使用一种较为简单的基于窗口的方案。我们首先设窗口的长度为 8,将任意一个数据以 8 个位元为一组进行分割。
假如我们的数据是 23243,其二进制表示为 0b101101011001011,我们将其分割的代码如下:
const W = 8;
export const splitEightBit = (n: bigint) => {
const windows = 16 / W;
const mask = BigInt(2 ** W - 1);
const shiftBy = BigInt(W);
for (let w = 0; w < windows; w++) {
let wbits = Number(n & mask);
n >>= shiftBy;
console.log(wbits.toString(2));
}
};
返回的结果为:
11001011
1011010
我们希望将上述数据使用 $\text{NAF}_{2^7}(k)$ 进行表示,所以我们需要将上述分组进行转化使用 $2^7$ 进行表示。我们约定每一个分组只能转化为一个位元。这里有读者发现了一个问题,我们使用的 $2^7$ 是与 8 位元的 $2^8$ 不匹配,所以理论上存在部分数据无法转化。我们采用 NAF 的处理方案,当遇到无法使用 $2^7$ 表示的数据时,我们进行进位操作,并将当前位元设置为负数。修改后的代码如下:
const W = 8;
export const splitEightBit = (n: bigint) => {
const windows = 16 / W;
const mask = BigInt(2 ** W - 1);
const wsize = 2 ** (W - 1);
const maxNum = 2 ** W;
const shiftBy = BigInt(W);
for (let w = 0; w < windows; w++) {
let wbits = Number(n & mask);
n >>= shiftBy;
if (wbits > wsize) {
wbits -= maxNum;
n += 1n;
}
console.log(wbits.toString(2));
}
};
输出结果如下:
-110101
1011011
可以使用 (0b1011011 << 8) - 0b110101 进行验算,发现结果一致。我们将上述输出结果转化为十进制表示:
-53(2**0)
91(2**8)
这些数值并不大,括号内表明的是当前数据所在的位元位置。我们上面编写的代码实际上存在某一些问题,我们尝试使用 0b1111111111111111 。该数字实际上是最大的 16 位数字,我们尝试使用 splitEightBit 对该数字进行分割,分割结果如下:
-1
0
我们发现这个输出肯定不正确,这是因为我们使用当前算法会通过进位与负数结合的方法。我们需要增加一个窗口,即修改 const windows = 16 / W + 1;。修改代码后我们就可以获得正常的输出:
-1
0
1
所以我们可以考虑直接预计算获得这些数值。我们可以尝试生成如下预计算数据
1(2**0) 2(2**0) 3(2**0) ... 2**7(2**0)
1(2**8) 2(2**8) 3(2**8) ... 2**7(2**8)
...
1(2**windows) 2(2**windows) 3(2**windows) ... 2**7(2**windows)
1(2**(windows+1) 2(2**(windows+1)) 3(2**(windows+1)) ... 2**7(2**(windows+1))
我们发现如果将上述数据拼接成一个数组,我们可以直接使用索引获得相关数据。比如对于 -53 ,我们只需要获得上述预计算数据的第 53 个数据,然后取反即可。我们首先编写这个预计算函数:
const { BASE: G, ZERO: I } = Point;
const precompute = () => {
const points: Point[] = [];
const windows = 256 / W + 1;
let p = G,
b = p;
for (let w = 0; w < windows; w++) {
b = p;
points.push(b);
for (let i = 1; i < 2 ** (W - 1); i++) {
b = b.add(p);
points.push(b);
}
p = b.double();
}
return points;
};
完成上述预计算后,我们可以直接使用需要在 splitEightBit 引入一些代码计算预计算数组的索引。我们可以使用以下代码进行索引计算:
const off = w * wsize;
const off2 = off + Math.abs(wbits) - 1;
console.log(`wbits: ${wbits} off: ${off2}`);
上述代码比较简单,我们使用 off 跳过一定数量的索引到指定窗口进行检索,然后使用 off + Math.abs(wbits) - 1 定位到所需要的索引,此处使用 Math.abs 的原因是存在负数的情况。完成以上工作后,我们只需要将索引获得数据按照正负情况累加即可。我们首先需要在 Point 类型内部实现取反函数,如下:
negate() {
return new Point(this.x, mod(-this.y));
}
完成以上取反函数后,我们就可以将代码如下:
let Gpows: Point[] | undefined = undefined;
export const wNAF = (n: bigint): { p: Point } => {
const comp = Gpows || (Gpows = precompute());
const neg = (cnd: boolean, p: Point) => {
let n = p.negate();
return cnd ? n : p;
};
let p = I;
const windows = 256 / W + 1;
const mask = BigInt(2 ** W - 1);
const wsize = 2 ** (W - 1);
const maxNum = 2 ** W;
const shiftBy = BigInt(W);
for (let w = 0; w < windows; w++) {
let wbits = Number(n & mask);
n >>= shiftBy;
if (wbits > wsize) {
wbits -= maxNum;
n += 1n;
}
const off = w * wsize;
const off2 = off + Math.abs(wbits) - 1;
if (wbits !== 0) {
p = p.add(neg(wbits < 0, comp[off2]));
}
}
return { p };
};
上述代码内引入了 neg 函数,其目的是根据 wbits 的情况对检索出的数值进行选择性取反操作。我们也引入了 Gpows 变量来保存预计算获得的数值。上述代码也将 windows 修改为正确的对 256 位数字进行划分窗口操作。
完成上述代码后,我们可以将 Point 内的 multiplyDA 修改为如下代码:
multiplyDA(n: bigint): Point {
return wNAF(n).p;
}
然后,我们可以使用 bun test 进行测试,会发现测试可以完全通过。然后可以执行 bun run bench/multiply.ts 进行性能测试并检查是否存在计时攻击问题,结果如下:
benchmark avg (min … max) p75 p99 (min … top 1%)
------------------------------------------- -------------------------------
small 474.27 ns/iter 417.00 ns █
(291.00 ns … 423.42 µs) 1.38 µs ▁▅█▂▂▂▁▁▂▁▁▁▁▁▁▁▁▁▁▁▁
big 32.57 µs/iter 32.87 µs █ █
(30.77 µs … 34.24 µs) 33.68 µs █▁▁▁▁▁▁▁███▁████▁▁▁▁█
我们可以看到显著的数量级的提升,函数执行速度从原有的 ms 级别优化到了 ns 甚至 µs 级别。接下来,我们需要处理计时攻击问题,简单来说,计时攻击发生在以下部分:
if (wbits !== 0) {
p = p.add(neg(wbits < 0, comp[off2]));
}
由于上述代码对空窗没有处理,所以出现运行时间不一致的问题。换句话说,在密码学编程中,任何出现分支的情况,我们都需要保证各分支内的计算情况一致。在上述代码内,我们并没有处理 wbits == 0 的情况,这导致 wbits == 0 的分支并不需要算法。
我们加入以下代码来处理另一个分支:
if (wbits === 0) {
f = f.add(neg(w % 2 !== 0, comp[off]));
} else {
p = p.add(neg(wbits < 0, comp[off2]));
}
此处的 f 定义为 let f = G;,而 w % 2 !== 0 仅是为了算力平衡,不会出现取反函数从不被调用的情况。补充以上代码后,我们重新执行性能测试,结果如下:
benchmark avg (min … max) p75 p99 (min … top 1%)
------------------------------------------- -------------------------------
small 901.09 µs/iter 963.13 µs ▃██
(752.67 µs … 1.36 ms) 1.33 ms ▅████▅▄▅▅▄▃▂▂▂▂▂▂▂▂▂▁
big 918.45 µs/iter 970.63 µs █▆ ▂
(757.88 µs … 1.38 ms) 1.33 ms ▆███▅▆██▇▄▃▁▂▂▂▂▃▂▂▂▁
由此我们完成了预计算的优化。
Jacobian projective coordinates
在上文中,我们不难发现进行 add 算法内的 invert 计算是一个相当不确定的因素,因为该算法使用了 GCB 算法,我们希望使用一种方案去掉求逆计算。在 Guide to Elliptic Curve Cryptography 内存在以下这样一段话:
If inversion in K is significantly more expensive than multiplication, then it may be advantageous to represent points using projective coordinates.
在此处,我们选择了将目前的 $(x, y)$ 仿射到 Jacobian coordinates 内部。所谓仿射(affine) 其实就是将二维 $(x, y)$ 内的点转化为三维空间 $(\lambda x, \lambda y, \lambda)$ 内,其中 $\lambda$ 为一个变量。从可视化理解,其实就是将二维平面内的点转化为三维空间内的线:
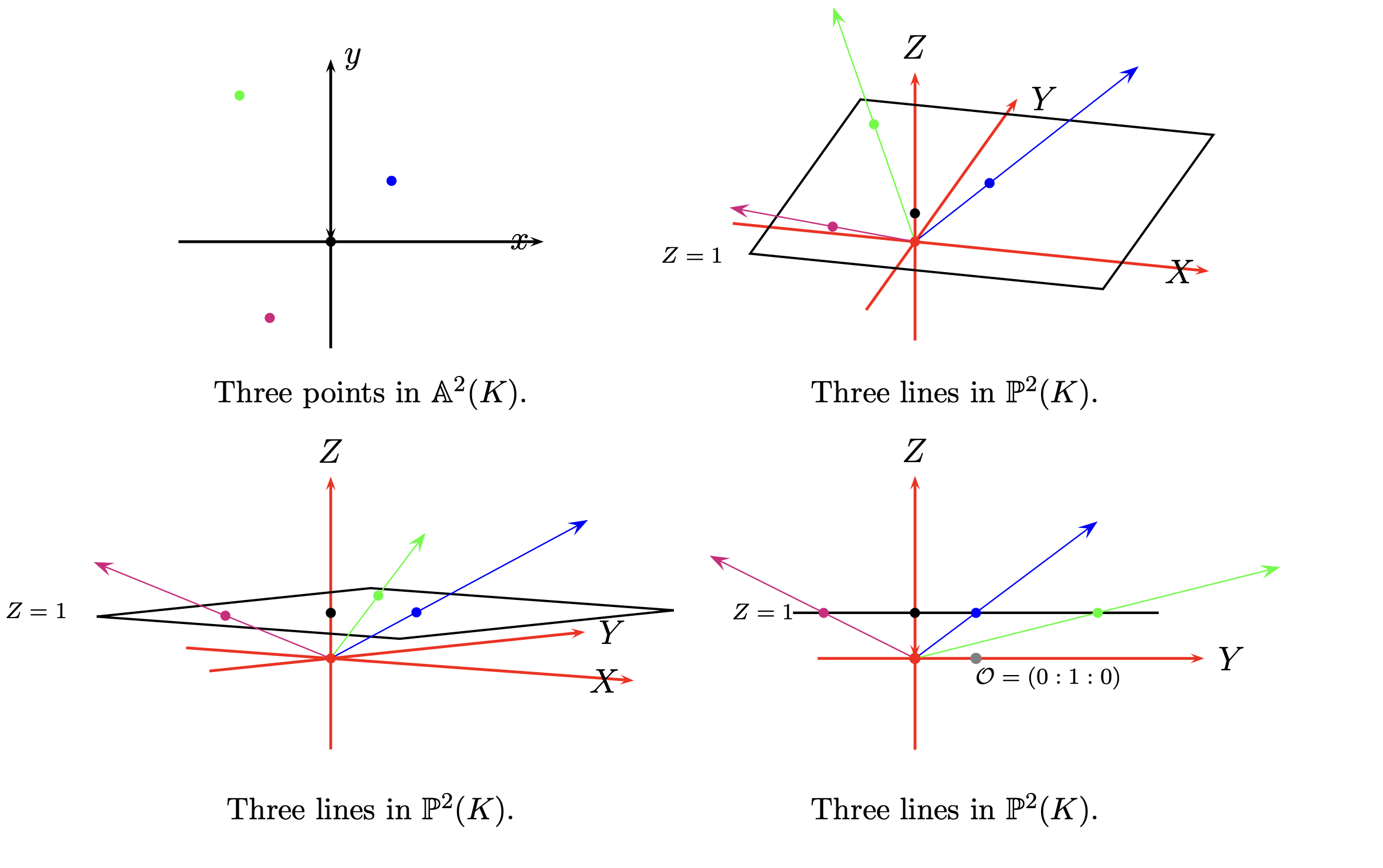
我们在进行仿射时往往选择将 $\lambda = 1$,那么 $(x, y)$ 的仿射结果为 $(x, y, 1)$。需要注意在 Jacobian coordinates 内,零点被定义为 $(0, 1, 0)$。
本文为了简化,没有介绍零点的具体来源。实际上如何定义椭圆曲线上的零点也并不是一个简单的问题
我们希望所有的计算都在 Jacobian coordinates 内进行,所以我们需要修改 Point 类型,为其增加 z 属性并增加仿射转化接口。我们首先处理从 $(x, y)$ 进行仿射到 Jacobian coordinates 的转化:
export class Point {
static readonly BASE = new Point(CURVE.Gx, CURVE.Gy, 1n);
static readonly ZERO = new Point(0n, 1n, 0n);
constructor(
readonly px: bigint,
readonly py: bigint,
readonly pz: bigint,
) {}
static fromAffine(p: AffinePoint) {
return p.x === 0n && p.y === 0n ? Point.ZERO : new Point(p.x, p.y, 1n);
}
}
接下来,我们增加一个函数用于判断点与点是否相等。基于仿射的转化方案,判断 $(x_1, y_1, z_1)$ 与 $(x_2, y_2, z_2)$ 相等的计算如下: $$ \frac{x_1}{z_1} = \frac{x_2}{z_2} \Rightarrow x_1z_2 = x_2z_1 \\ \frac{y_1}{z_1} = \frac{y_2}{z_2} \Rightarrow y_1z_2 = y_2z_1 $$ 当同时满足上述两个条件后,我们可以称 $(x_1, y_1)$ 和 $(x_2, y_2)$ 相等。转化为如下代码:
equals(other: Point): boolean {
const { px: X1, py: Y1, pz: Z1 } = this;
const { px: X2, py: Y2, pz: Z2 } = other;
const X1Z2 = mod(X1 * Z2),
X2Z1 = mod(X2 * Z1);
const Y1Z2 = mod(Y1 * Z2),
Y2Z1 = mod(Y2 * Z1);
return X1Z2 === X2Z1 && Y1Z2 === Y2Z1;
}
接下来,我们可以编写从 $(x,y,z)$ 转化为 $(x,y)$ 的函数方法:
toAffine(): AffinePoint {
const { px: x, py: y, pz: z } = this;
if (this.equals(I)) return { x: 0n, y: 0n };
if (z === 1n) return { x, y };
const iz = invert(z);
if (mod(z * iz) !== 1n) throw new Error("invalid inverse");
return { x: mod(x * iz), y: mod(y * iz) };
}
aff() {
return this.toAffine();
}
get x() {
return this.aff().x;
}
get y() {
return this.aff().y;
}
negate() {
return new Point(this.px, mod(-this.py), this.pz);
}
在上述代码内,我们也补充了 negate 函数以实现取反。
完成上述工作后,我们需要为当前的 Point 方法修正 add 函数和 double 函数。这里我们直接使用 Complete addition formulas for prime order elliptic curves 内给出的相关算法:

直接将上述伪代码直接转化为代码即可:
add(other: Point) {
const { px: X1, py: Y1, pz: Z1 } = this;
const { px: X2, py: Y2, pz: Z2 } = other;
let X3 = 0n,
Y3 = 0n,
Z3 = 0n;
const b3 = mod(21n);
let t0 = mod(X1 * X2), // 1
t1 = mod(Y1 * Y2), // 2
t2 = mod(Z1 * Z2), // 3
t3 = mod(X1 + Y1), // 4
t4 = mod(X2 + Y2); // 5
t3 = mod(t3 * t4); // 6
t4 = mod(t0 + t1); // 7
t3 = mod(t3 - t4); // 8
t4 = mod(Y1 + Z1); // 9
X3 = mod(Y2 + Z2); // 10
t4 = mod(t4 * X3); // 11
X3 = mod(t1 + t2); // 12
t4 = mod(t4 - X3); // 13
X3 = mod(X1 + Z1); // 14
Y3 = mod(X2 + Z2); // 15
X3 = mod(X3 * Y3); // 16
Y3 = mod(t0 + t2); // 17
Y3 = mod(X3 - Y3); // 18
X3 = mod(t0 + t0); // 19
t0 = mod(X3 + t0); // 20
t2 = mod(b3 * t2); // 21
Z3 = mod(t1 + t2); // 22
t1 = mod(t1 - t2); // 23
Y3 = mod(b3 * Y3); // 24
X3 = mod(t4 * Y3); // 25
t2 = mod(t3 * t1); // 26
X3 = mod(t2 - X3); // 27
Y3 = mod(Y3 * t0); // 28
t1 = mod(t1 * Z3); // 29
Y3 = mod(t1 + Y3); // 30
t0 = mod(t0 * t3); // 31
Z3 = mod(Z3 * t4); // 32
Z3 = mod(Z3 + t0); // 33
return new Point(X3, Y3, Z3);
}
double() {
return this.add(this);
}
完成上述代码后,读者可以自行修复一下代码内的报错,然后执行测试,如果上述代码编写正确会发现所有测试都可以通过,然后执行 bun run bench/multiply.ts 可以获得如下结果:
benchmark avg (min … max) p75 p99 (min … top 1%)
------------------------------------------- -------------------------------
small 123.86 µs/iter 125.08 µs █▆▅
(104.33 µs … 561.75 µs) 172.71 µs ▃▂▆███▇▆▄▃▃▂▂▁▁▁▁▁▁▁▁
big 124.96 µs/iter 126.08 µs █▅█▂
(106.13 µs … 567.71 µs) 163.79 µs ▁▂▅████▇▅▅▄▃▂▂▁▁▁▁▁▁▁
比之前的版本加速了 10 倍,这是因为在 precompute 内,我们使用椭圆曲线上的加法和倍增算法。由于我们使用了更新的算法,所以这部分预计算被进一步加速。
签名和验证
基础算法
在上文内,我们一直介绍的基本都与私钥计算公钥有关,始终没有涉及签名和验证环节。在本节中,我们将向读者介绍如何使用以上代码进行签名和验证。
我们首先介绍一下椭圆曲线密码学签名和验证的基础原理。签名流程如下:
- 使用随机数生成器获得一个位于 $k \in [1,N−1]$。此处的 $N$ 为一个常数
- 计算 $kG = (x_1, y_1)$,并计算 $r = x_1 \mod N$
- 计算 $s = k^{-1}(m + dr) \mod N$。此处的 $m$ 指需要签名的数据,而 $d$ 代表用户的私钥
此时,用户可以对外给出 $r$ 和 $s$ 作为自己的签名。当然,此时签名验证者也知道用户的公钥 $Q$。那么验证者如何验证用户正确使用了私钥进行签名呢?我们可以做如下推导: $$ s = k^{-1}(m + dr) \mod N \Leftrightarrow k = s^{-1}(m + dr) \mod N $$ 上述推导实际上就是两侧同时乘以 $k$ 然后除以 $s$ 即可。
有了上述推导后,我们可以继续如下计算: $$ \begin{align} k &= s^{-1}(m + dr) = s^{-1}m + s^{-1}dr \\ &\Leftrightarrow kG = s^{-1}mG + s^{-1}rdG = s^{-1}mG + s^{-1}rQ \end{align} $$ 由此,我们只需要验证 $kG = s^{-1}mG + s^{-1}rP$。事实上,由于我们不知道 $kG$ 的具体坐标,但知道 $kG$ 坐标的 $x$ 值为 $r$。所以最后验证的是 $s^{-1}mG + s^{-1}rP$ 的横坐标 $x$ 与 $r$ 相等。
在这里读者会发现,假如我们假设用户的签名正确,是可以在签名内恢复公钥的。这是因为 $s^{-1}$ 和 $r$ 都可以根据签名计算。但是我们只知道 $kG$ 的横坐标,而 secp256k1 的曲线是关于 x 轴对称的,所以理论上会计算出两种 $y$ 值,其中一个为正值,而另一个为负值,这对于确定性计算公钥造成了麻烦。还有另一个麻烦,
r值有可能是被修正过的,因为我们计算r的时候使用了mod算法,所以我们也需要确定性获得r的数值。为了解决此问题,我们引入了 $v$ 值,该值用于计算公钥。这也是大家一般见到签名都包含r / s / v的原因。
在相当多的文献内,都会使用 $w = s^{−1} \mod N$ , $u_1 = mw \mod N$ 和 $u_2 = rw \mod N$ 的表述。由此,许多文献都会在验证过程中,要求验证者计算 $X = u_1G + u_2Q$ ,并验证 $X$ 的横坐标与 $r$ 相等。这与我们上文的表述是一致的。最后,我们附上一个学术化的表述:

上图内部分表述与我们的表述不同,请读者自行处理
k 值计算
接下来,我们需要处理一个问题,即 $k$ 如何生成?在这里不加解释的给出一个原则:假如 $k$ 值被复用或者可以被获取,那么用户的私钥可以直接被破解。假如我们知道某一个用户签名的 $k$ 值,可以直接使用一下方法计算出该用户的私钥: $$ d = r^{-1}(ks - m) \mod N $$ 如果用户在两笔签名内使用了同一个 $k$,我们可以使用一下方法计算获得 $k$ 然后使用刚刚给出的公式计算私钥: $$ k = (s_1 - s_2)^{-1}(m_1 - m_2) \mod N $$
关于 $k$ 值的计算,在 RFC6979 内有一个非常详细的文档介绍。在此处,我们简单介绍一下:
- 将待签名的数据的哈希值
H(m)记为h1 - 设置
v为全部由0x01构成的与哈希值与h1长度相同的数组。由于一般使用SHA256算法,所以v一般是由 32 个0x01构成 - 设置
k为全部由0x00构成的与哈希值与h1长度相同的数组 - 使用
HMAC算法计算K = HMAC_K(V || 0x00 || int2octets(d) || bits2octets(h1))。其中d代表用户的私钥,而int2octets算法可以认为将数字转化为十六进制字符串,然后转化为对应的字节。而HMAC_K指使用k作为密钥进行 HMAC 操作 - 计算
V = HMAC_K(V) - 计算
K = HMAC_K(V || 0x01 || int2octets(x) || bits2octets(h1)),此处的x实际上就是h1 - 计算
V = HMAC_K(V) - 此时设
k = V进行签名计算,但是k并不一定满足签名的条件,所以此处我们需要使用循环直到生成合适的k为止,循环过程中计算V = HMAC_K(K || V)
上文的第 8 步参考了 noble-secp256k1 源代码。
noble-secp256k1的实现与 RFC6979 有所不同。
接下来,我们进行具体的 $k$ 值计算的编码工作。在 RFC6979 A.1.2. Generation of k 内给出了相关的示例,但是该示例使用了一条 163 位的曲线,与我们的 secp256k1 曲线并不相符。
我们首先实现计算 int2octets(x) 的函数。在实现之前,我们需要知道 int2octets(x) 的工作原理。该函数会比较 x 的长度 blen 和 椭圆曲线的阶 qlen(我们可以认为是一个常数,在 secp256k1 内是 256)。当 qlen < blen 时,int2octets(x) 函数会将 x 的最左侧保留,丢弃右侧位,换言之,即将 x >> (blen - qlen) 位,使其长度等同于 qlen。而当 qlen > blen 时,int2octets(x) 函数将直接返回 x 的值。
我们首先实现一个辅助函数,将十六进制字符串转化为 Uint8Array 类型(在后文,我们称其为 Bytes 类型):
type Bytes = Uint8Array;
const hexToBytes = (hex: string): Bytes => {
const l = hex.length;
const arr = new Uint8Array(l / 2);
for (let i = 0; i < arr.length; i++) {
const j = i * 2;
const h = hex.slice(j, j + 2);
const b = Number.parseInt(h, 16);
arr[i] = b;
}
return arr;
};
原理很简单,就是从输入的十六进制字符串内按照顺序每次抽取 2 个数字放到 arr 数组内即可。为什么抽取 2 个数字?是因为 Bytes 数组内每一个数字应该是 8 位,而一个十六进制字符只有 4 位。在此处,为了方便,我们也实现上述函数的逆函数,即将 Bytes 类型转化为十六进制的工具函数和 Bytes 转化为 BigInt 的函数:
const padh = (n: number | bigint, pad: number) =>
n.toString(16).padStart(pad, "0");
const bytesToHex = (b: Bytes): string =>
Array.from(b)
.map((e) => padh(e, 2))
.join("");
const bytesToBigInt = (b: Bytes): bigint =>
BigInt("0x" + (bytesToHex(b) || "0"));
最后,我们就可以实现 bits2int 函数:
const bits2int = (bytes: Uint8Array): bigint => {
const delta = bytes.length * 8 - 256;
console.log(`Bytes Length: ${bytes.length}`);
const num = bytesToBigInt(bytes);
return delta > 0 ? num >> BigInt(delta) : num;
};
接下来,我们需要实现 int2octets(d) 函数。这个函数其实等同于直接将类型为 bigint 的 d 转化为 Bytes 类型。我们可以使用以下代码实现:
const bigintToBytes = (num: bigint): Bytes => {
return hexToBytes(padh(num, 2 * fLen));
};
我们的 generateK 函数最终被暂时定义为以下代码:
export const generateK = (msg: string, priv: bigint) => {
const h1i = mod(bits2int(hexToBytes(msg)), N);
const h1o = hexToBytes(padh(h1i, 2 * fLen));
const seed = [bigintToBytes(priv), h1o];
return seed;
};
接下来,我们要实现一系列 HMAC_K 操作。在此处,我们使用了 bun 标准库内的 HMAC 算法。当然,读者也可以使用 Web Crypto API 内的方法。
const hmacSha256 = async (key: Bytes, ...msgs: Bytes[]) => {
const hasher = new Bun.CryptoHasher("sha256", key);
hasher.update(concatBytes(...msgs));
return new Uint8Array(hasher.digest());
};
如果读者使用
bun内的标准库函数,请务必执行bun upgrade命令,因为旧版本的bun并没有实现此函数。
接下来,我们实现上文介绍的 k 值计算的具体函数:
export const generateK = async (msg: string, priv: bigint) => {
const h1i = mod(bits2int(hexToBytes(msg)), N);
const h1o = hexToBytes(padh(h1i, 2 * fLen));
const seed = concatBytes(bigintToBytes(priv), h1o);
let v = new Uint8Array(fLen);
let k = new Uint8Array(fLen);
let i = 0;
const reset = () => {
v.fill(1);
k.fill(0);
i = 0;
};
const h = (...b: Bytes[]) => hmacSha256(k, v, ...b);
const reseed = async () => {
k = await h(new Uint8Array([0x00]), seed); // k = hmac_K(V || 0x00 || seed)
v = await h(); // v = HMAC_K(v)
k = await h(new Uint8Array([0x01]), seed); // k = hmac_K(V || 0x01 || seed)
v = await h();
};
const gen = async () => {
if (i++ >= 1000) throw new Error("drbg: tried 1000 values");
v = await h();
return v;
};
};
此处,我们引入了 h 作为辅助函数。然后,gen 函数用于反复测试以生成合理的 k 值。事实上,此处的 generateK 还缺少一部分,因为我们需要判断 k 值是否合理。在判断 k 值的前提是我们需要实现真正的签名算法。
签名
签名部分并不复杂,由于签名函数是需要私钥的,我们考虑减少用户将私钥作为参数传递的次数,所以此处我们考虑首先将 generateK 内使用私钥作为参数的第一部分转移到签名函数内部。最终结果如下:
const moreThanHalfN = (n: bigint): boolean => n > N >> 1n;
export const prepSig = (msg: string, priv: bigint, lowS = true) => {
const h1i = mod(bits2int(hexToBytes(msg)), N);
const h1o = hexToBytes(padh(h1i, 2 * fLen));
const seed = concatBytes(bigintToBytes(priv), h1o);
const m = h1i;
const k2sig = (kBytes: Bytes) => {
const k = bits2int(kBytes);
if (k > CURVE.n) return;
const ik = invert(k, N);
const q = G.multiplyDA(k).aff(); // q = kG
const r = mod(q.x, N);
if (r === 0n) return;
const s = mod(ik * mod(m + mod(priv * r, N), N), N);
if (s === 0n) return;
let normS = s;
let rec = (q.x === r ? 0 : 2) | Number(q.y & 1n);
if (lowS && moreThanHalfN(s)) {
normS = mod(-s, N);
rec ^= 1;
}
return new Signature(r, normS, rec);
};
return { seed, k2sig };
};
我们使用 seed 存储数据。在 k2sig 内部,我们完成了签名的具体逻辑。在此处,我们不再赘述签名的具体流程,在上文内,我们已经给出了相关流程。在此处,我们主要关注一下两个问题:
lowS的作用。lowS实际上来源于 bitcoin 交易签名。在有限域内,mod(s, N)与mod(-s, N)实际上是相同的。这就导致同一个签名同时存在两个有效的s。这造成了所谓的延展性问题,即当节点拿到用户的交易后,节点可以通过修改s的方式影响交易内容。所以 Bitcoin 网络在v0.9.0后认为lowS,即小于s < N / 2的签名交易才正常。目前,所有交易都采用了lowS形式。关于lowS和highS的占比情况,可以参考 此网站rec作用。在本节第一部分,我们就讨论了r参数的作用。该参数的目标是为了实现从签名中只可以恢复出唯一的用于签名的公钥。我们会在后文介绍公钥恢复时再次提及此参数。
接下来,我们完成所有的函数:
type Pred = (v: Uint8Array) => Signature | undefined;
export const hmacDrbg = () => {
let v = new Uint8Array(fLen);
let k = new Uint8Array(fLen);
let i = 0;
const reset = () => {
v.fill(1);
k.fill(0);
i = 0;
};
const h = (...b: Bytes[]) => hmacSha256(k, v, ...b);
const reseed = async (seed: Bytes = new Uint8Array()) => {
k = await h(new Uint8Array([0x00]), seed); // k = hmac_K(V || 0x00 || seed)
v = await h(); // v = HMAC_K(v)
k = await h(new Uint8Array([0x01]), seed); // k = hmac_K(V || 0x01 || seed)
v = await h();
};
const gen = async () => {
if (i++ >= 1000) throw new Error("drbg: tried 1000 values");
v = await h();
return v;
};
return async (seed: Bytes, pred: Pred) => {
reset();
await reseed(seed);
let res: Signature | undefined = undefined;
while (!(res = pred(await gen()))) await reseed();
reset();
return res!;
};
};
export const signZero = async (
msgh: string,
priv: bigint,
lowS = true,
): Promise<Signature> => {
const { seed, k2sig } = prepSig(msgh, priv, lowS);
return hmacDrbg()(seed, k2sig);
};
上述 hmacDrbg 函数实际上就是之前编写的 generateK 函数。我们通过外部参数注入和函数注入完成了最终的签名。然后,我们可以编写如下测试与官方签名进行对比:
test("sign", async () => {
const privKey = utils.randomPrivateKey();
const privBigint = bytesToBigInt(privKey);
const msgHash =
"b94d27b9934d3e08a52e52d7da7dabfac484efe37a5380ee9088f7ace2efcde9";
const signatureExpect = await signAsync(msgHash, privKey);
const signature = await signZero(msgHash, privBigint);
expect(signature.r).toBe(signatureExpect.r);
expect(signature.s).toBe(signatureExpect.s);
expect(signature.recovery).toBe(signatureExpect.recovery);
});
如果不出意外的话,测试可以正常通过。在此处,我们没有深入介绍如何生成一个高度随机的私钥,该部分内容读者可以自行参考 noble-secp256k1 的实现,其核心随机数来源自 WebCrypto 自带的 getRandomValues 函数。
如果读者对随机数生成感兴趣,可以考虑阅读 链上随机数生成:理论与实现 一文。
验证
在上一节内,我们介绍了如何签名。在本节内,我们将介绍如何使用代码实现签名验证。我们首先需要为 Point 实现一个完整的 mul 方法:
mul(n: bigint, safe = true): Point {
if (this.equals(G)) return wNAF(n).p;
let p = I,
f = G;
for (let d: Point = this; n > 0n; d = d.double(), n >>= 1n) {
if (n & 1n) p = p.add(d);
else if (safe) f = f.add(d);
}
return p;
}
mulAddQUns(R: Point, u1: bigint, u2: bigint): Point {
return this.mul(u1, false).add(R.mul(u2, false));
}
我们在 mul 函数内增加了 safe 参数,该参数用于配置是否启用抗计时攻击。而 mulAddQUns 函数则封装了 $X = u_1G + u_2Q$ 部分。有了上述函数,我们可以非常简单的实现一个 verify 函数:
export const verifyZero = async (
sig: Signature,
publicKey: Point,
msgh: string,
lowS = true,
) => {
if (lowS && moreThanHalfN(sig.s)) return false;
const h = mod(bits2int(hexToBytes(msgh)), N);
let R: AffinePoint;
try {
const w = invert(sig.s, N);
const u1 = mod(h * w, N);
const u2 = mod(sig.r * w, N);
R = G.mulAddQUns(publicKey, u1, u2).aff();
} catch (e) {
return false;
}
const v = mod(R.x, N);
return v === sig.r;
};
对于该函数的测试,读者可以自行完成。限于篇幅,本文并没有引入公钥的编解码规则,所以此处直接使用 Point 类型。
公钥恢复
公钥恢复是一个对于区块链非常重要的属性。当用户将交易及其签名发送给区块链网络时,网络内的节点会默认签名正确然后使用签名推导出签名人的公钥并进行进一步的共识确认。所以说,我们需要一种方案从签名内恢复出用户的公钥,并保证恢复出的公钥是唯一的。
我们首先进行恢复私钥的数学推导,已知: $$ \begin{align} kG = &R = s^{-1}mG + s^{-1}rQ \Leftrightarrow \\ &Rsr^{-1} = mr^{-1}G + Q \Leftrightarrow \\ &Q = sr^{-1}R - mr^{-1}G \end{align} $$ 我们将 $kG$ 所在的点记为 $R$。为了简单,我们仍记 $u_1 = -mr^{-1}$ 和 $u_2 = sr^{-1}$。如此,我们可以记 $Q = u_1G + u_2R$
接下来,我们需要具体判断某些数的值:
R = kG的正负问题。由于我们最终拿到的只有R的横坐标,由于在有限域内计算r时,使用了const r = mod(q.x, N);的算法,所以r与R的横坐标不一定相同。此时当recovery = 2时,我们认为坐标不一致,使用r + N作为q.x的真实值。- 在确认
q.x后,计算出的R的y坐标可能存在正负两种可能。此时当recovery & 1 = 0时,说明y的值为正,否则为负数。注意在下文内,我们虽然称q.y > 0或q.y < 0,但实际上在secp256k1有限域内不存在负数,但存在奇偶性。我们要求计算获得的奇偶性和R.y的奇偶性一致。
上述判断也解释了为什么我们会在签名函数 k2sig 内使用 let rec = (q.x === r ? 0 : 2) | Number(q.y & 1n); 计算 recovery 的值。总结一下,recovery 的值可能有以下四种情况:
recovery = 0,此时q.x = r和q.y为奇数成立recovery = 1,此时q.x = r和q.y为偶数成立recovery = 2,此时q.x != r和q.y为奇数成立recovery = 3,此时q.x != r和q.y为偶数成立
正如上文所述,我们在此处将
q.y > 0和q.y < 0转化为了更加严谨的表述
简单来说,recovery 的第二位决定 q.x 和 r 的关系,而第一位决定 q.y 的奇偶性。
在进行具体的分解之前,我们会发现目前还不会进行有限域上的开方计算。对于开方计算,有以下几种算法:
- 对于任意的开方计算,可以使用 Tonelli–Shanks algorithm 算法,该算法较为复杂
- 对于特殊的数值的开方计算,可以使用 ModPow 算法
由于 secp256k1 曲线选择的 p + 1 是 4 的倍数,所以我们可以使用 ModPow 算法,该算法指出:
$$
sqrt(a) = a^{\frac{p+1}{4}}
$$
编写如下求 sqrt 的代码:
const sqrt = (n: bigint) => {
let r = 1n;
for (let num = n, e = (CURVE.P + 1n) / 4n; e > 0n; e >>= 1n) {
if (e & 1n) r = (r * num) % CURVE.P;
num = (num * num) % CURVE.P;
}
if (mod(r * r) !== n) {
throw new Error("sqrt invalid");
}
return r;
};
上述算法实际上类似之前最开始介绍的计算 kG 的算法。我们的目标是计算 num ^ ((p + 1) / 4) 的数值。为了降低计算复杂度,我们使用了 num * num 来加速计算,并最终视奇偶性(e & 1n) 来判断是否需要多乘一个 num。
接下来,我们为 Point 增加一个 fromX 的方法:
static fromX(x: bigint, headOdd: Boolean): Point {
let p: Point | undefined = undefined;
let y = sqrt(crv(x));
const isYOdd = (y & 1n) === 1n;
if (headOdd !== isYOdd) y = mod(-y);
p = new Point(x, y, 1n);
return p;
}
简单来说,当发现 sqrt 返回的结果与指定的 headOdd 不一致时,我们将执行取反操作。
我们可以为该函数增加如下测试:
test("point from x", async () => {
const privKey = utils.randomPrivateKey();
const publicKey = ProjectivePoint.fromPrivateKey(privKey);
const publicPoint = new Point(
publicKey.px,
publicKey.py,
publicKey.pz,
).toAffine();
const pointFromX = Point.fromX(
publicPoint.x,
(publicPoint.y & 1n) === 1n,
).toAffine();
expect(pointFromX.y).toBe(publicPoint.y);
});
在 Signature 对象内增加以下方法:
recoverPublicKey(msgh: string): Point {
const { r, s, recovery: rec } = this;
if (![0, 1, 2, 3].includes(rec!)) throw new Error("recovery id invalid");
const h = mod(bits2int(hexToBytes(msgh)), N);
const radj = rec === 2 || rec === 3 ? r + N : r;
if (radj >= CURVE.P) throw new Error("q.x invalid");
const headOdd = (rec! & 1) === 0 ? false : true;
const R = Point.fromX(radj, headOdd);
const ir = invert(radj, N);
const u1 = mod(-h * ir, N);
const u2 = mod(s * ir, N);
return G.mulAddQUns(R, u1, u2);
}
该方法的流程如下:
- 使用
rec === 2或rec === 3的情况修复r值,将其修复为真正的R点的横坐标 - 使用
rec! & 1操作判断R点的纵坐标的奇偶性,此处注意与fromX内部的定义对应 - 最终使用 $Q = u_1G + u_2R$ 计算复原公钥
对于以上代码,我们可以编写如下测试:
test("recovery public point", async () => {
const privKey = utils.randomPrivateKey();
const publicKey = ProjectivePoint.fromPrivateKey(privKey);
const publicPoint = new Point(publicKey.px, publicKey.py, publicKey.pz);
const msgHash =
"b94d27b9934d3e08a52e52d7da7dabfac484efe37a5380ee9088f7ace2efcde9";
const signature = await signAsync(msgHash, privKey);
const signatureZero = new Signature(
signature.r,
signature.s,
signature.recovery,
);
const publicPointRecovery = signatureZero.recoverPublicKey(msgHash);
expect(publicPoint.x).toBe(publicPointRecovery.x);
expect(publicPoint.y).toBe(publicPointRecovery.y);
});
由此就完成了公钥的恢复。
未解决的问题
在本文中,我们已经实现了大部分关于 secp256k1 曲线的核心内容,但本文没有涉及一下几个方面:
- 编码与解码。通常情况下,我们看到的公钥和私钥都是十六进制字符串,这是使用一些特定的编码方式获得的,该部分内容读者可以自行参考源代码
- ECDH 方面。secp256k1 曲线也可以用于 ECDH 来协商加密通信。这部分内容我们也没有在文章内具体介绍。但该部分内容比较简单
- 边缘情况处理。本文所编写的代码相比于 noble-secp256k1 缺少了较多的边界条件处理,缺少边界条件处理可能导致安全问题,读者可以自行阅读源代码来处理边界条件。本文尽可能保留了核心参数的边界条件检查。