概述
在 上一篇文章 中,我们介绍了常见的几种有理多项式插值方法,但我们并没有给出具体的 Huff 语言实现及其测试。本文仍考虑在智能合约内实现以下公式:
$$ f(x) = e^x $$
与上一篇文章不同,本文不会进一步讨论具体的插值原理,而是主要介绍插值的实现及其误差测试。
建议读者在阅读本文前,可以阅读笔者所写的另一篇关于 huff 数学函数优化的文章,即Huff实战:编写测试极致效率数学模块
准备
本文仍将是有笔者最喜欢的 huff 框架进行开发,因为这种数学函数预期将会被高频调用,所以使用 huff 实现可以提高 gas 效率。
读者应确保本地已安装最新版本的 huff 和 forge ,可以使用以下命令更新:
huffup
foundryup
使用以下命令初始化项目:
forge init --template https://github.com/huff-language/huff-project-template huff_approximation
初始化项目后,使用 forge test 进行测试,如果测试通过,即说明项目初始化成功。
我们需要安装高精度计算工具来实现任意精度的计算:
pip install mpmath
当然,读者也可以继续使用 gmpy2 和 flame 组合进行任意精度的计算,此处使用 mpmath 的原因在于其设置精度较为方便。
在本文中,我们假设用户使用 18 位定点小数,且数据类型为 int256 。对于拟合一个多项式,我们一般需要遵循以下 5 个步骤:
计算下溢出界和上溢出界,此处需要注意定点小数问题
将 $10^{-18}$ 定点小数输入转化为 $2 ^ {-96}$ 定点小数
对于 $e^x$ 这种输入范围较大的函数,我们需要压缩输入空间,利用 2 的幂将其压缩到 $[-\frac{1}{2}ln2, \frac{1}{2}ln2]$
使用拟合多项式计算结果
将输出结果从 $2 ^ {-96}$ 定点小数重新转化为 $10^{-18}$ 定点小数
在接下来的文章内,我们会依次介绍上述五个步骤。
上下溢出界计算
首先计算下溢出界和上溢出界,简单来说,就是计算以下方程:
$$ \begin{gather} e^x \le &0.5 \times 10^{-18} \\ e^x \ge & (2^{255} - 1) \times 10^{-18} \end{gather} $$
上述 $(1)$ 式用于计算拟合下界 $x_{min}$,当 $x \le x_{min}$ 时,我们可以认为 $e^x = 0$ 。而 $(2)$ 式用于计算 $x_{max}$ 。当 $x \ge x_{max}$ 时,我们可以给出溢出报错。
此处需要注意我们对 $0.5$ 和 $2^{255} - 1$ 都进行除以 $10^{-18}$ 的操作,这是为了方便我们在常规的浮点数系统内进行各项计算。
使用 python 计算如下:
>>> from mpmath import mp
>>> mp.dps = 100
>>> mp.log(0.5e-18) * 1e18
mpf('-42139678854452767550.19865425115481035552649055042768341446365801675243961682794242714604085622045646871')
>>> mp.log((2 ** 255 - 1)* 1e-18) * 1e18
mpf('135305999368893231660.612768842138391071801543845797661640430424413556327607413904767954970854862727543')
为了提高计算精度,我们使用 mp.des 将 mpmath 的计算结果的精度提高到小数点后 100 位。此处我们需要将结果转化为 18 位定点小数的表示方法。简单来说,就是将原本的计算结果与 $10^{18}$ 相乘,取整数部分作为后续编程使用的部分。
我们可以将上述结果转化为 16 进制形式:
cast to-int256 -- -42139678854452767550
cast to-int256 135305999368893231660
输出结果依次为 0xfffffffffffffffffffffffffffffffffffffffffffffffdb731c958f34d94c2 和 0x0755bf798b4a1bf22c 。
我们可以编写此部分的代码:
#define macro EXP_WAD(fail) = takes (1) returns (1) {
0xfffffffffffffffffffffffffffffffffffffffffffffffdb731c958f34d94c2
dup2 // [x, 0xfff..., x]
sgt iszero // [x <= 0xfff..., x]
ret_zero jumpi // [x]
0x0755bf798b4a1bf22c // [0x0755bf798b4a1bf22c, x]
dup2 // [x, 00755bf798b4a1bf22c, x]
slt iszero // [x >= 0755bf798b4a1bf22c, x]
<fail> jumpi // [x]
...
ret_zero:
0x00 dup1 mstore
0x20 0x00 return
}
上述 huff 代码给出了上下界的检测代码。
精度拓展与压缩
我们需要将用户输入的 x 从 $10^{-18}$ 定点小数输入转化为 $2^{-96}$ 定点小数。该步骤的作用是尽可能提高后续的计算精度。
该转换方法如下:
$$ x * 2^{96} / 10^{18} \rArr x * 2^{78}/5^{18} $$
上述公式可以转化为以下 huff 代码:
0x03782dace9d9 // [0x05 ** 0x12, x]
swap1 // [x, 0x05 ** 0x12]
0x4e shl // [x << 0x4e, 0x05 ** 0x12]
sdiv // [x << 0x4e / 0x05 ** 0x12]
之后,我们需要进行本文最难理解的操作,即压缩操作。$e^x$ 定义域过于庞大,我们无法在如此大的定义域范围内进行高效的插值操作。所以,我们会通过 2 的幂进行定义域的压缩。
众所周知,在二进制系统内计算 2 的幂是相当简单的,我们可以通过位移快速计算,而 2 的幂与 e 的幂具有一定的关系,我们可以进行如下推导:
$$ e^x = y \rArr e^x = e^{x’} \cdot 2^k = y $$
此处,我们希望 $x’$ 的值尽可能小,所以我们要求 $k$ 值是使 $2^k$ 与 $e^x$ 最接近的的值,我们可以通过以下方法计算:
$$ 2^k = e^x \rArr k ln2 = x \rArr k = \frac{x}{ln2} $$
由于我们使用了二进制系统,事实上,$k = round(\frac{x}{ln2})$ 。此处的 $round()$ 函数的作用是对 $\frac{x}{ln2}$ 进行四舍五入,将其转化为最近的整数。基于上述计算,我们可以使用 $k$ 进一步计算出 $x’$ 的值,如下:
$$ e^{x’} = \frac{e^x}{2^k} \rArr e^{x’} = \frac{e^x}{e^{kln2}} \ \rArr e^{x’} = e^{x-kln2} \rArr x’ = x - kln2 $$
此处我们需要计算 $x’$ 的取值范围,这对于我们后期进行多项式差值非常重要,计算如下:
基于 $round$ 函数性质,我们可以做以下判断:
$$ -\frac{1}{2} \le \frac{x}{ln2} - k \le \frac{1}{2} $$
在以上不等式两侧同乘以 $ln 2$ 即可获得如下结论:
$$ -\frac{1}{2} ln2 \le x’ \le \frac{1}{2} ln2 $$
此时,我们只需要计算 $e^{x’}$ 和 $k$ 的值,即可获得最终的 $e^x$ 的值。指定注意的是,此时 $x’$ 的取值范围是一个较小的范围,我们可以相对简单的进行多项式插值。
此处我们需要计算 $ln2$ 的值:
>>> from mpmath import mp
>>> mp.dps = 100
>>> mp.log(2) * 2 ** 96
mpf('54916777467707473351141471128.0154260805001742877543849979355656005268225665434638061337873130637291434807195749013124401134212796741196786240755259301995292746610664043288579469023157658164821289269505639409486471315172910372456063029589221012379723954364902007614255203407273001340128185595237247415465')
此处我们给出的 $x$ 和 $x’$ 都定义在 $2^{96}$ 定点小数下,所以我们需要将计算出的 $ln2$ 的数值与 $2^{96}$ 相乘,由此计算出 huff 程序中所需要的数字。
使用 cast 命令进行以下转化:
cast to-int256 54916777467707473351141471128
使用 solidity 实现 $k$ 和 $x’$ 的计算如下:
int256 k = ((x << 96) / 0xb17217f7d1cf79abc9e3b398 + 2**95) >> 96;
x = x - k * 0xb17217f7d1cf79abc9e3b398;
此处为了实现对 $k$ 的高精度计算,我们将 $x$ 值左移了 96 位,同时为了完成四舍五入的任务,此处在原始计算值的基础上增加了 2**95 因子。
我们给出 $k$ 和 $x’$ 的计算代码:
0xb17217f7d1cf79abc9e3b398
dup2 // [x, 0xb17217f7d1cf79abc9e3b398, x]
0x60 shl // [x << 96, 0xb17217f7d1cf79abc9e3b398, x]
sdiv // [x << 96 / 0xb17217f7d1cf79abc9e3b398, x]
0x7ffffff20f9306d2eea00000 // [2**95, x << 96 / 0xb17217f7d1cf79abc9e3b398, x]
add // [2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398, x]
0x60 sar // [(2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96, x]
dup1 // [(2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96, (2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96, x]
0xb17217f7d1cf79abc9e3b398
mul // [((2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96) * 0xb17217f7d1cf79abc9e3b398, (2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96, x]
dup3 // [x, ((2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96) * 0xb17217f7d1cf79abc9e3b398, (2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96, x]
sub // [x (new), (2**95 + x << 96 / 0xb17217f7d1cf79abc9e3b398) >> 96, x]
swap2 pop // [k, x]
多项式插值
拟合过程中,需要使用 flamp 和 gmpy2 提高计算精度。相关代码如下:
import numpy as np
import baryrat
import flamp
import gmpy2
flamp.set_dps(100)
f = np.vectorize(gmpy2.exp)
r = baryrat.brasil(f, interval=(-0.5 * gmpy2.log(2), 0.5 * gmpy2.log(2)), deg=6)
拟合结果如下图:
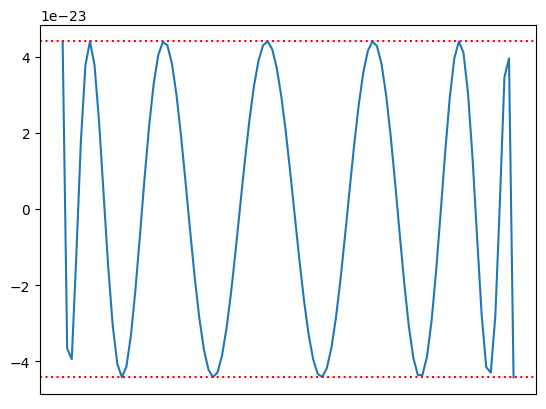
我们拟合 6 阶有理多项式插值结果在有效区间内达到了 1e-23 的精度,这对于 1e-18 精度的 solidity 定点浮点数计算而言是足够精度的。接下来,我们需要导出参数并编写对应的 huff 代码。我们在此给出 barycentric rational 的公式形式:
$$ r(x) = \frac{\sum_{i=0}^{n} \frac{w_i}{x - x_i}f_i}{\sum_{i=0}^{n}\frac{w_i}{x-x_i}} $$
$x_i$ 获得方法如下:
r.nodes * 2 ** 96
此处与 $2^{96}$ 相乘是为了拓展精度。
输出结果为:
array([mpfr('-27247190619124229480851962779.14421508523297455388622727338673152819748568003417589787265682743756711011',336),
mpfr('-22355066305703376974991507851.61763303491999212323815684785490114058832845686984069380799058812128284283',336),
mpfr('-12177908192722921420825317509.82886443989503428701473658530228778702365048950104401184905638328404522025',336),
mpfr('731674125066875208036172098.7184079710410375337109867547181533585470107420288276739988887759591054766799',336),
mpfr('13325506944415758094759208550.13918038640473340655709403663610531677903283680970282728513202145189665324',336),
mpfr('22827650200580638870993653771.23146530634681285831044598301343632690413485551634450940097646531057637729',336),
mpfr('27268464511175257421771730771.15750871723802041724863219986212732005670682269476998670927528640693863989',336)],
dtype=object)
使用 cast to-int256 可以轻松将其全部转换为 16 进制形式。
$w_i$ 的获得方法如下:
r.weights * 2 ** 96
而 $f_i$ 的获得方法如下:
r.values * 2 ** 96
我们首先给出 $\frac{w_i}{x - x_i}$ 部分计算的 huff 代码的生成模板:
def hex_output(x):
if x < 0:
return f"0x{int(x).to_bytes(32, byteorder='big', signed=True).hex()}"
else:
return hex(int(x))for i in range(len(r.nodes)):
for i in range(len(r.nodes)):
x = r.nodes[i] * 2 ** 96
w = r.weights[i] * 2 ** 192
print(f"""
{hex_output(x)}
dup{i+3} sub
{hex_output(w)}
sdiv""")
可能有读者好奇此处为什么 w = r.weights[i] * 2 ** 192 而不是仅乘以 2 ** 96 ,这是因为除法的原因。我们需要保证 $\frac{w_i}{x - x_i}$ 结果的精度为 $2^{96}$ ,而 $x - x_i$ 的精度也为 $2^{96}$ ,此时则需要 $w_i$ 放大至 $2^{192}$ 后才可以保证计算结果的正确。
输出内容如下:
0xffffffffffffffffffffffffffffffffffffffffa7f5a6f4d4b8a8fe3aa40465
dup3 sub
0xffffffffffffffffd752072ed36e7ed9c248c4e9e30953ded71ef67087dcf476
sdiv
0xffffffffffffffffffffffffffffffffffffffffb7c4529343d36e8e280d3e74
dup4 sub
0x6208c969dbc2dfea58b3f04d46a0e6332efb677515e780f6
sdiv
0xffffffffffffffffffffffffffffffffffffffffd8a6aba20e589715ebafaf7a
dup5 sub
0xffffffffffffffff86ab45463827cd1f88564b009d2c9bd2f510c3797ca1efdc
sdiv
0x25d3a05cc2579dd535ac143
dup6 sub
0x7eaaa8a1c0f898ab4f32764454d7c2168e6e7d134448a5bc
sdiv
0x2b0e99daee28ee21449da666
dup7 sub
0xffffffffffffffff8b17e4d3da07b495c74d5b324ae190ec2fdf830c663b4048
sdiv
0x49c296f502abd59f23bc500b
dup8 sub
0x5bcaadab3d0b3bd9c116bfa91d02a9a811d13684d76f6f8c
sdiv
0x581bf1f72b025a21f7906f53
dup9 sub
0xffffffffffffffffda6caeff74ae791befdfeb11435f5729bea17fd9f81bb224
sdiv
经历上述计算后,我们可以获得如下栈结构:
[z7, z6, z5, z4, z3, z2, z1, k, x]
其中 $z_i$ 指 $\frac{w_i}{x - x_i}$ 计算的结果。
通过简单的累加计算可以完成分母的计算:
dup1 dup3 add // [z6 + z7, z7, z6, z5, z4, z3, z2, z1, k, x]
dup4 add // [z5 + z6 + z7, z7, z6, z5, z4, z3, z2, z1, k, x]
dup5 add // [z4 + ... + z7, z7, z6, z5, z4, z3, z2, z1, k, x]
dup6 add // [z3 + ... + z7, z7, z6, z5, z4, z3, z2, z1, k, x]
dup7 add // [z2 + ... + z7, z7, z6, z5, z4, z3, z2, z1, k, x]
dup8 add // [z_sum, z7, z6, z5, z4, z3, z2, z1, k, x]
swap7 // [z1, z7, z6, z5, z4, z3, z2, z_sum, k, x]
在累加计算的最后,我们通过 swap7 将分母移动到了栈的最后,这为下面的分子计算预留了空间,同时也方便最终使用分子与分母相除计算结果。
在此处我们首先计算 ${z_1}f_1$ 的值,然后依次计算 $z_7f_7$ 等多项式的值。此处我们可以使用以下 Python 代码自动生成对应的 huff 源代码:
values_filp = np.flip(r.values)
values_filp[0], values_filp[-1] = values_filp[-1], values_filp[0]
for i in range(len(values_filp)):
value_hex = hex_output(values_filp[i] * 2 ** 96)
if i == 0:
print(f"{value_hex} mul add")
else:
print(f"swap1 {value_hex} mul add")
生成的 huff 代码如下,注意,为了方便读者理解,此处的栈注释是我自己手动编写的:
0xb580a548e650e58875b0beec mul // [zf1, z7, z6, z5, z4, z3, z2, z_sum, k, x]
swap1 0x1692bfda80c72f9ce8f6680ae mul add // [zf1 + zf7, z6, z5, z4, z3, z2, z_sum, k, x]
swap1 0x1557c15c88ccaf93baf9e591c mul add // [zf1 + zf6 + zf7, z5, z4, z3, z2, z_sum, k, x]
swap1 0x12ee3c8d76e6524a23e077f4e mul add // [zf1 + zf5 + zf6 + zf7, z4, z3, z2, z_sum, k, x]
swap1 0x1026007a88c5ca9b866f440ff mul add // [zf1 + zf4 + zf5 + zf6 + zf7, z3, z2, z_sum, k, x]
swap1 0x0db86a7517b76d59b3c86ca36 mul add // [zf1 + zf3 + zf4 + zf5 + zf6 + zf7, z2, z_sum, k, x]
swap1 0x0c110244aaacf876b955c86ec mul add // [zf_sum, z_sum, k, x]
可能有读者好奇此处的 mul 是否会导致溢出?在前文中,我们将 $x$ 压缩到了一个较为狭小的区间,此处不会因为溢出而对结果有影响。
最后,使用除法获得分子与分母的商:
sdiv
此处我们没有将分子乘以 $2^{96}$ 是因为 $z_if_i$ 已经为 $2^{192}$ 精度而无需手动进行精度拓展处理。
最后,我们需要将结果从 $2^{96}$ 的精度转化为 $10^{18}$ 。此流程只需要将结果先乘以 $10^{18}$ 然后除以 $2^{96}$ 即可,对应的 huff 代码如下:
0xde0b6b3a7640000
mul // [0xde0b6b3a7640000 * r, k, x]
0x60 sar // [r, k, x]
swap1 // [k, r, x]
shl // [r, x]
一些 Debug 经验
在进行拟合过程中,我们其实不太可能会非常顺利的一次性完成所有 huff 代码,可能会遇到一系列问题。对于大部分问题,我们都可以通过 foundry 提供的 debug 解决。
首先需要编写对应函数的测试,比如:
function testSetAndGetValue() public {
uint256 value = simpleExp.getValue(0.5 ether);
console.log(value);
assertEq(value, 1648721270700128146);
}
我们可以通过以下命令触发对此函数的 debug:
forge test --debug testSetAndGetValue
进入 debug 页面后,我们需要按下 C 键跳转进入 huff 调用环节:
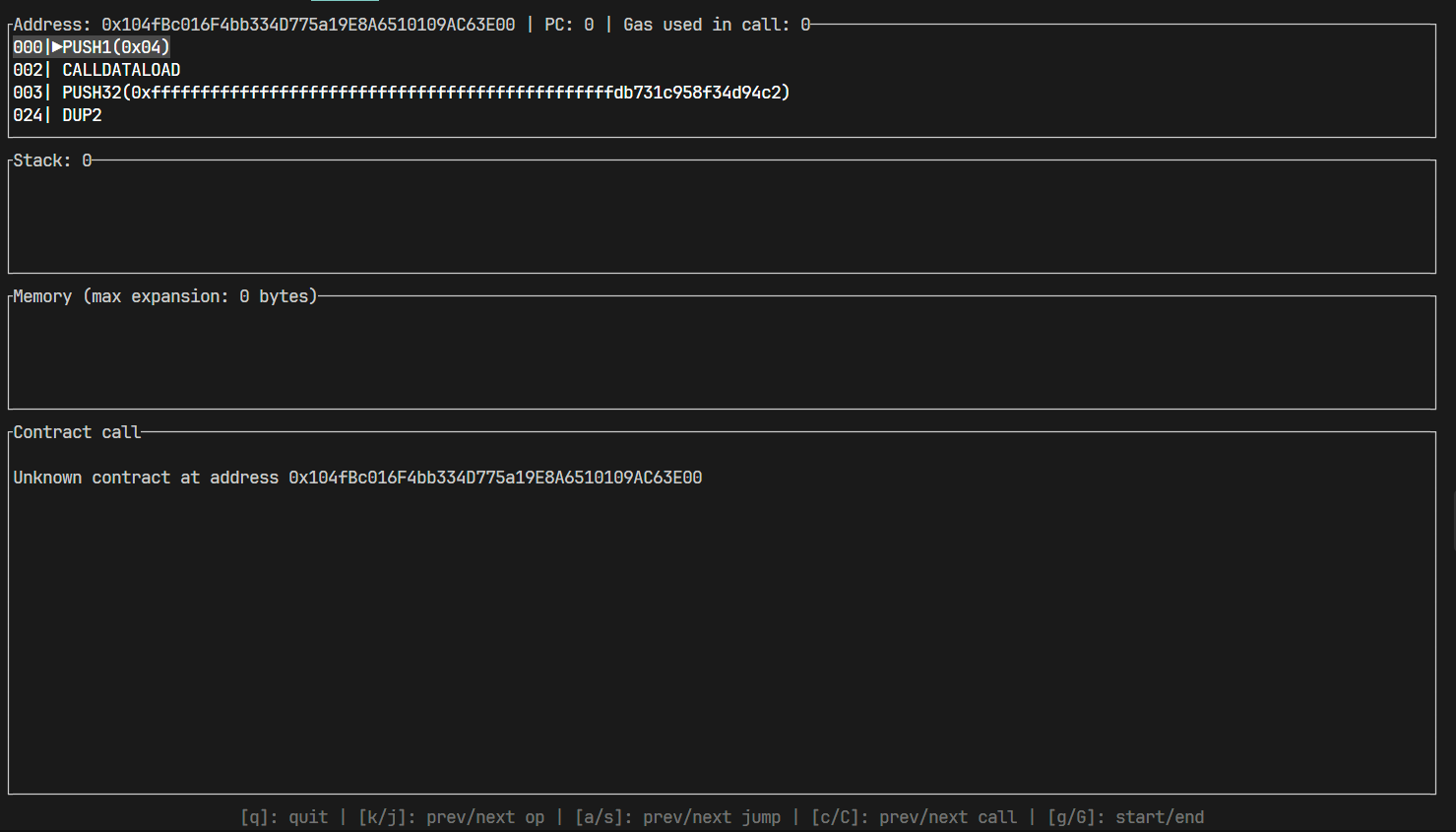
接下来,我们一般需要校验以下几个内容:
- 栈内的元素数量是否正确
- 栈内数据的顺序是否正确,往往需要在
swap后检查。可能需要按下J向上滚动栈元素或者K向下滚动栈元素 - 每个式子的计算结果是否符合预期。我们可以使用
mpmath模块在 python 内计算出预期结果转化为 16 进制与栈内的数据进行比较,判断结果是否正确
一般来说,应当优先检查 1 和 2 项,最后检查 3 项。
实际误差测试
在编写完 huff 智能合约后,我们需要对其进行实际的运行测试,考虑到大部分编写的 huff 代码都较为简单,且考虑到使用 python 生态与前文的拟合是搭配的,所以本文决定使用 python 进行实际运行测试。
在 Python 中执行 EVM 字节码的一个比较好的选择是 smol-evm 库,该库实现了一个较为简单的 EVM 且基本支持了所有 opcode 操作码。如果读者关心 EVM 运行问题,可以选择使用一系列使用 rust 实现的 EVM 库,但是笔者考虑到开发速度,还是选择了 smol-evm 作为 EVM 执行库。
我们首先需要获得 Huff 文件对应的字节码,使用 huffc src/<filename>.huff --bin-runtime 命令可以获得 src/<filename>.huff 对应的字节码。
然后,读者需要在本地使用 pip install smol-evm 安装 smol-evm 包,建议读者使用 venv 虚拟环境。
获得 huff 文件对应的字节码并安装完 smol-evm,进行以下编程即可实现 huff 字节码执行:
from smol_evm.opcodes import *
from smol_evm.runner import run
code = bytes.fromhex("670de0b6b3a764000060243560601b046004358015610019575b906c01199999999999a000000000000260601d5b670de0b6b3a76400000260601d5f5260205ff3")
def hex_output(x):
return hex(int(x))[2:].zfill(64)
def zero_evm(x):
calldata = bytes.fromhex("742daebd" + hex_output(0) + hex_output(x))
return int(run(code, calldata=calldata).returndata.hex(), 16)
print(zero_evm(1.3321e18))
此处我们测试了一个简单的 huff 函数,此函数签名如下:
function getValue(uint256, uint256) external returns (uint256);
当然,此处的函数名可以任意选择,该函数的作用是当第一个参数为 0 时,会将第二个参数放大 1.1 倍。此处我们使用 "742daebd" + hex_output(0) + hex_output(x) 构造出指定的 calldata 来输入 EVM 环境。
如果读者第一次使用
smol-evm可以使用run(code, calldata=calldata, verbose=True).returndata.hex(),使用verbose标识后,会输出字节码执行过程中的具体操作
接下来,我们进行严格的测试,代码如下:
import pandas as pd
import numpy as np
import flamp
import gmpy2
from smol_evm.opcodes import *
from smol_evm.runner import run
flamp.set_dps(100)
code = bytes.fromhex("670de0b6b3a764000060243560601b046004358015610019575b906c01199999999999a000000000000260601d5b670de0b6b3a76400000260601d5f5260205ff3")
def hex_output(x):
return hex(int(x))[2:].zfill(64)
def zero_evm(x):
calldata = bytes.fromhex("742daebd" + hex_output(0) + hex_output(x * 1e18))
return int(run(code, calldata=calldata).returndata.hex(), 16)
x = flamp.linspace(0, 1000, 10000)
y = x * 1.1
evm_array = []
for i in x:
evm_array.append(gmpy2.mpfr(zero_evm(i)) / 1e18)
evm_array = np.array(evm_array)
diff = y - evm_array
diff.max()
diff.min()
我们使用了 flamp 来增加系统的精度,选择了 [0, 1000] 内的 10000 个不同的数值点进行计算,最终获得的最大误差为 1.54766e-18 ,该误差基本不会影响最终的计算结果和用户体验。
总结
对于任一复杂函数的 huff 近似,我们一般需要遵循以下步骤:
- 求解上下界,避免运算过程中出现溢出
- 精度拓展,一般需要将 $10^{18}$ 拓展至 $2^{96}$ ,值得注意的是,精度拓展会对除法和乘法产生影响
- 压缩输入,我们可以根据函数的性质,尝试引入 2 的幂来压缩输入的范围
- 多项式插值,使用各种方法进行多项式插值
- 生成 huff 代码,一般来说,我们可以通过多项式直接生成对应的 huff 代码