概述
VRGDA(Variable Rate GDAs) 是一种渐进式荷兰式拍卖(Gradual Dutch Auctions, GDAs)的扩展,其作用是在超长代币发行期间保持一个合理价格的且定期的流动性释放。而普通的 GDAs 则是只可以保证代币出售的价格合理,但不能保证代币在合适的时间释放。
本文将首先介绍渐进式荷兰式拍卖 GDAs,然后引入 VRGDA。本文主要参考了 Gradual Dutch Auctions 和 Variable Rate GDAs 文章,相比于上述两篇文章,本文的介绍增加了一定数学的推导,但对于 VRGDA 内较为复杂的 Logistic Issuance Schedule,本文并没有加以介绍。
渐进式荷兰式拍卖 GDAs
GDAs 被分为以下两类:
- 离散 GDA(Discrete GDA)
- 连续 GDA(Continuous GDA)
我们会在后文以此介绍上述两种拍卖方案,最终也会给出其 solidity 合约实现。
在介绍渐进式 GDA 前,我们首先介绍常规的荷兰式拍卖方案,假如读者拥有 1000 个 NFT 需要出售,常规的荷兰式拍卖方案为直接打包 1000 个 NFT 作为一个整体集合,读者可以设定最高价格,随着时间的推移,NFT 集合的总体价格会逐渐下降,最终肯定存在一位购买者直接拍下整个 NFT 集合。这种方案显然是较难成交的,因为可能存在某一个意愿购买者只希望购买该集合内的某一个 NFT 而不是整个集合。
一个自然的想法是,我将 NFT 集合内每一个 NFT 都进行一次荷兰式拍卖,这样就可以大幅度降低成交难度,提高竞拍者的竞拍意愿。但对每一个 NFT 都进行一次荷兰式拍卖似乎 gas 消耗过高。
另一种自然的想法是,每一个 NFT 都在同一时间起拍,所有 NFT 的价格都可以根据下降率及当前时间计算。这种方式将大幅度降低 gas 费用,但是由于荷兰式拍卖的特点,会导致在任一时点所有未被拍出的 NFT 的价格是相同的,这大大降低了某一时点内的价格多样性,不利于价格发现。
离散 GDA
离散 GDA 就有效解决了上文的问题,其工作原理实际上是上述第二种方案的衍生。上述第二种方案解决了 gas 消耗问题,但是另一方面带来了单一时间点内的价格多样性下降。离散 GDA 引入了一个比例因子 $\alpha^{n}$ 来提高价格多样性,此处的 $n$ 可以认为是 NFT 的 tokenId。
离散 GDA 基于以下算法计算当前 NFT 集合内每一个 NFT 的价格:
$$ p_n(t) = k \cdot \alpha^{n} \cdot e^{-\lambda t} $$
其中,$k$ 为初始价格,$\alpha$ 为比例因子,$\lambda$ 为下降率,而 $t$ 为从起拍到计算时的时间差。
下图展示了 n = 1, 2, 3 的不同 NFT 在同一时间的价格,我们可以看到引入比例因子 $\alpha^{n}$ 后,同一时间内,不同的 NFT 的价格表现不同,且 tokenId 越大则价格越高,充分为用户提供了价格的多样性。
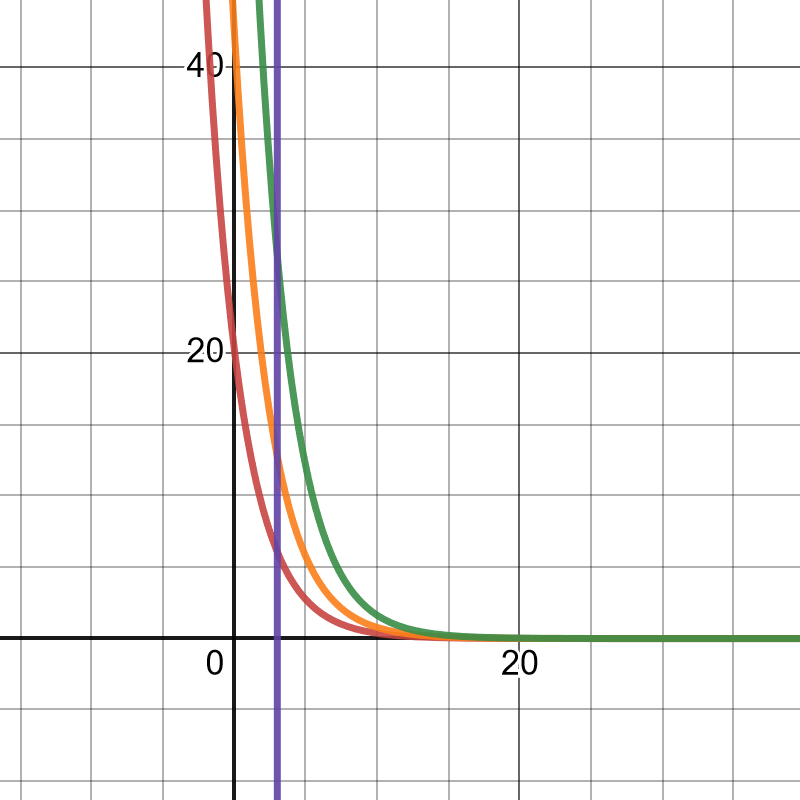
本图像也提供 交互版本
接下来,我们计算离散 GDA 的批量购买成本,设拍卖已经进行了 $T$ 秒,且已售出 $m$ 个 NFT,此时用户购入 $q$ 个 NFT,其花费的总价格如下:
$$ \begin{align} P(q) &= \sum_{m+q-1}^{n=m}p_n(T) \\ &= \sum_{m+q-1}^{n=m} k \cdot \alpha^n e^{-\lambda t} \\ &= k e^{-\lambda t} \sum_{m+q-1}^{n=m} \alpha^n \\ &= \frac{k \alpha^m(\alpha^q - 1)}{e^{\lambda T}(\alpha - 1)} \end{align} $$
上述 $(3)$ 到 $(4)$ 式的转化使用了等比数列的求和公式:
$$ Sn=a_1 \times (1-q^n)/(1-q) $$
下图展示了用户一次性购买不同数量的 NFT 所支付的总金额:
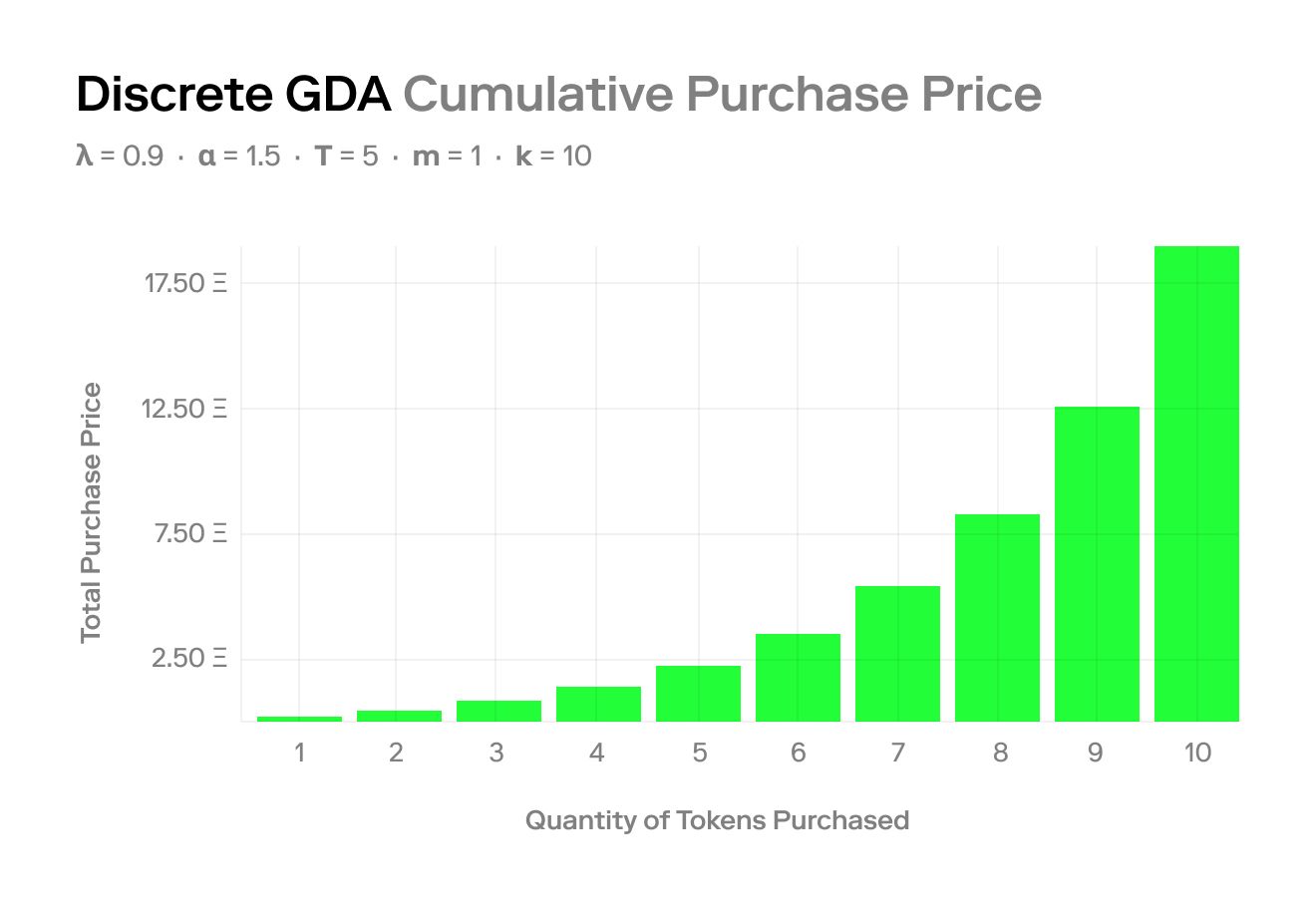
上述算法在 solidity 中的实现如下:
function purchasePrice(uint256 numTokens) public view returns (uint256) {
int256 quantity = int256(numTokens).fromInt();
int256 numSold = int256(currentId).fromInt();
int256 timeSinceStart = int256(block.timestamp).fromInt() -
auctionStartTime;
int256 num1 = initialPrice.mul(scaleFactor.pow(numSold));
int256 num2 = scaleFactor.pow(quantity) - PRBMathSD59x18.fromInt(1);
int256 den1 = decayConstant.mul(timeSinceStart).exp();
int256 den2 = scaleFactor - PRBMathSD59x18.fromInt(1);
int256 totalCost = num1.mul(num2).div(den1.mul(den2));
//total cost is already in terms of wei so no need to scale down before
//conversion to uint. This is due to the fact that the original formula gives
//price in terms of ether but we scale up by 10^18 during computation
//in order to do fixed point math.
return uint256(totalCost);
}
注意上述代码直接使用了 PaulRBerg/prb-math 库进行数学计算,此处使用的 PRBMathSD59x18 即带符号整数部分为 59 位且小数部分为 18 位的类型。该代码未经良好优化,使用时可选择其他的使用 yul 汇编优化的数学库进行计算。
连续 GDA
假如用户希望出售一定数量的同质化代币且需要控制每日代币排放量,我们该如何解决此问题?离散 GDA 无法解决此问题,因为离散 GDA 是没有办法控制每日代币排放量的。一个选择是,每分钟启动一次 1 个代币的标准荷兰式拍卖,但是这种方案会消耗大量 gas。
一个可行的优化方案如下:
我们假设无限细分代币,且对一份细分代币进行一次虚拟荷兰式拍卖,每份细分代币的价格可以使用以下函数确定:
$$ p(t) = k \cdot e^{- \lambda t} $$
此处的 $\lambda$ 为下降率,而 $t$ 为从起拍到计算时的时间差,而 $k$ 用于控制起拍价格。
而用户参与竞拍过程希望购买一定数额 $q$ 的代币,其支付的资金可以使用以下方法计算:
$$ \begin{align} P(q) &= \int^T_{T - \frac{q}{r}} p(t) dt \\ &= \int^T_{T - \frac{q}{r}} k \cdot e^{- \lambda t}dt \\ &= \frac{k}{\lambda} \cdot (e^{-\lambda(T-\frac{q}{r})}-e^{-\lambda}T) \\ &= \frac{k}{\lambda} \cdot \frac{e^{\frac{\lambda q}{r}}{} - 1}{e^{\lambda T}} \end{align} $$
此处的 $r$ 为代币释放率。下图展示了 $P(q)$ 的图像:
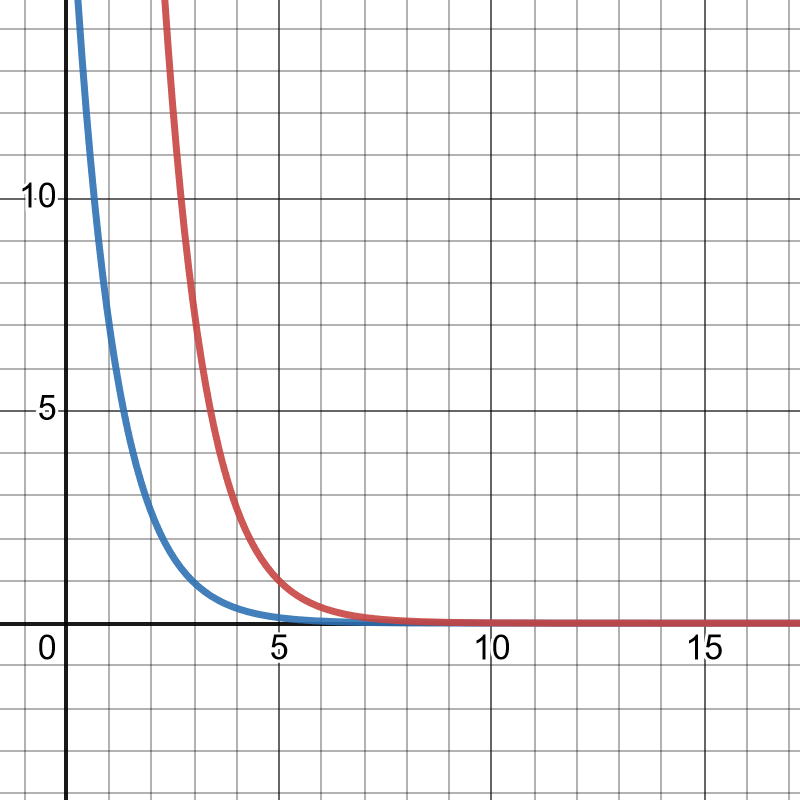
本图像也提供 交互版本
此图像中的蓝线代表购买 3 个代币的价格图像,而绿线代表购买 5 个代币的价格图像。
以下图像展示了用户在某一个时点购买多个代币所支付的总价格:
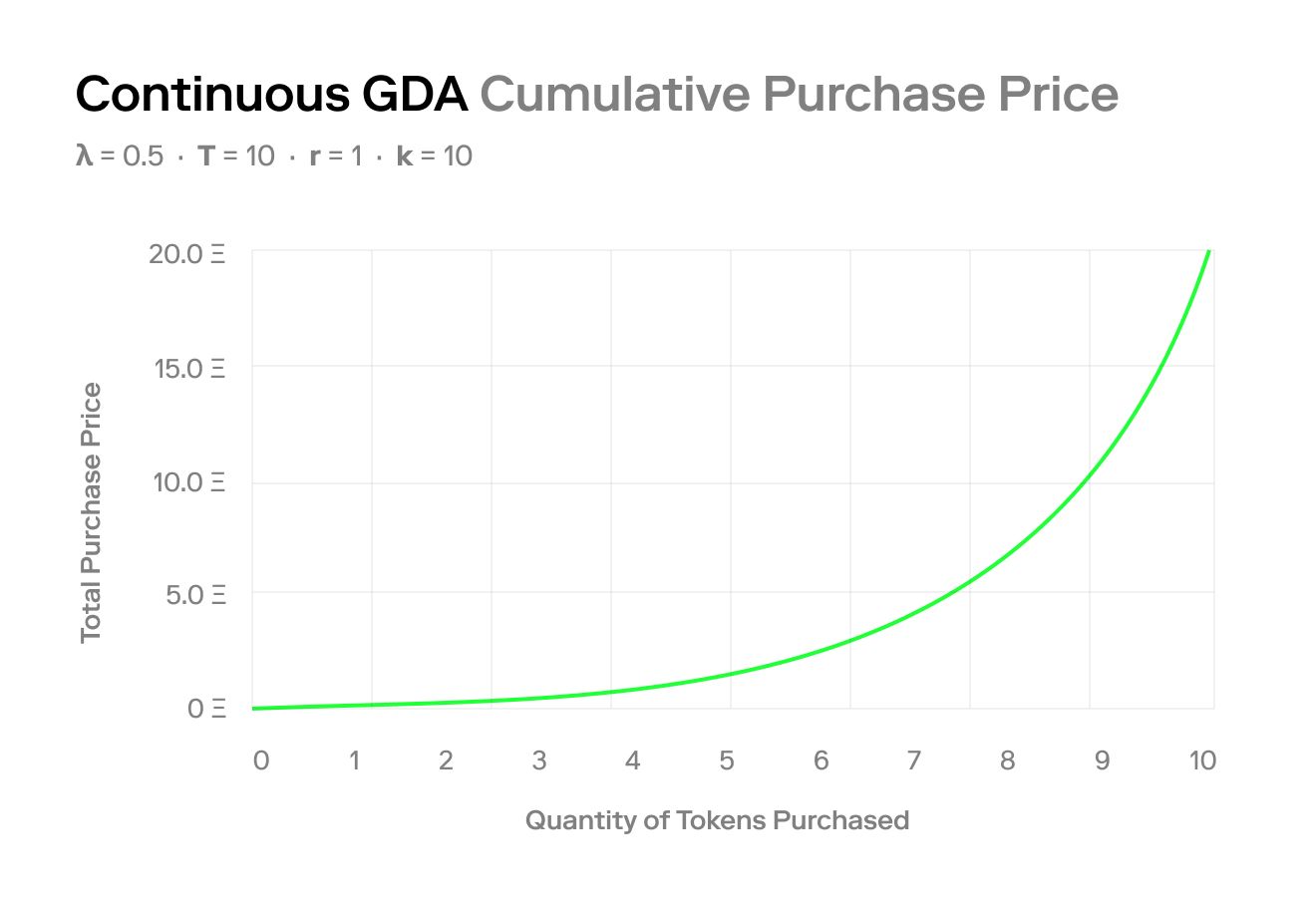
可变利率 GDA
上文介绍的离散 GDA 对于 NFT 释放没有调节作用。假设我们预期 NFT 每天售出 10 个,当前为拍卖第 5 天,此时预期售出 50 个 NFT,但我们发现市场上已售出了 70 个 NFT。此时,我们可以选择提高 NFT 价格至原价格的 $2^{\frac{70 - 50}{10}}$ 倍。
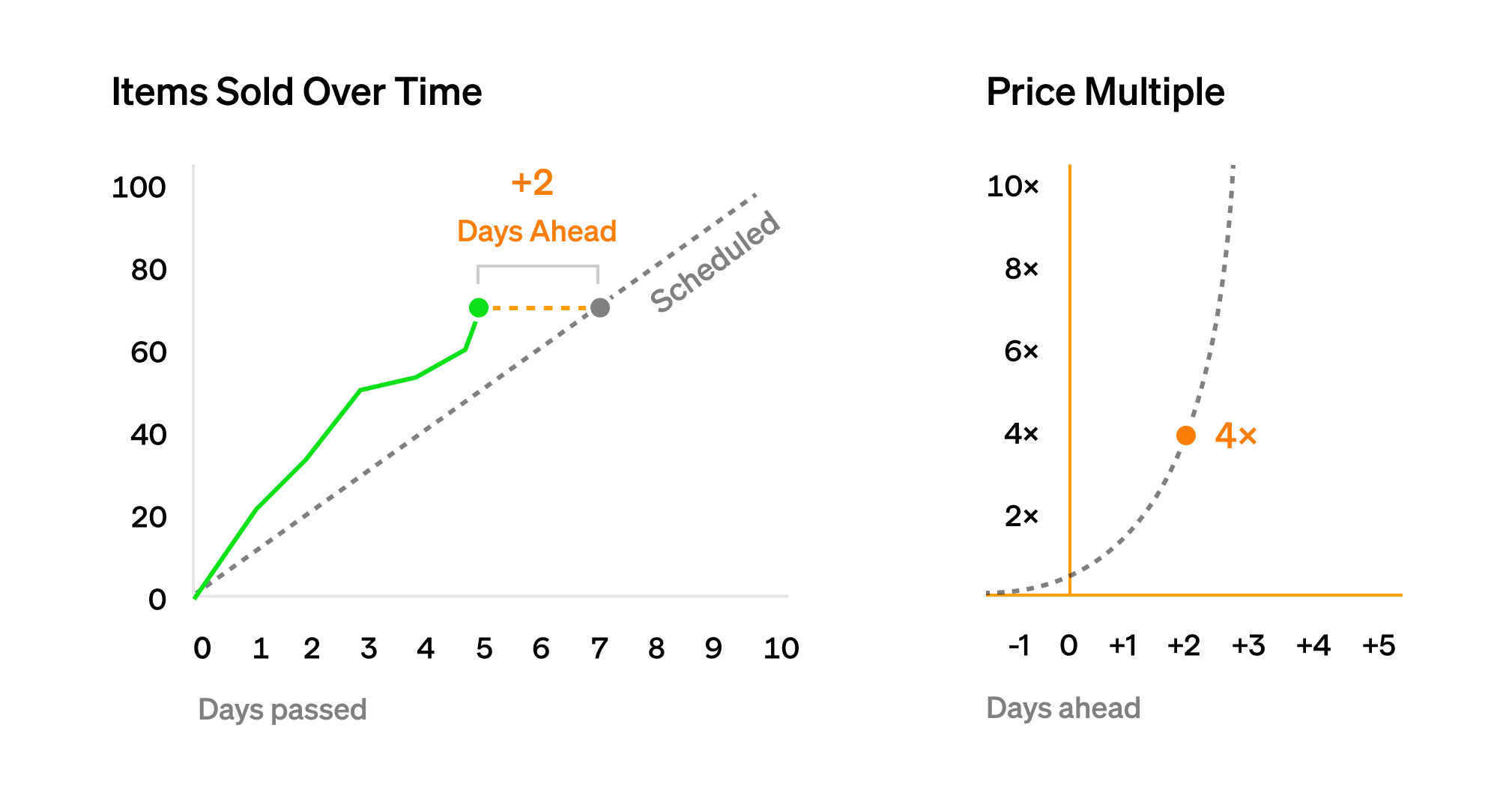
简单来说,我们通过对 GDA 的价格进行一次调整来实现调控 NFT 发行的目标。我们称这种调整后的 GDA 为 VRGDA。
我们尝试进行一些复杂的数学推导来计算调整因子:
- $p_0$ 完全按计划出售的目标价格
- $k$ 当 NFT 未被出售时,单位时间下降的百分比
- $f(t)$ 目标发行计划函数,计算当前时间预期发行的数量
假设每 2 天发行一个 NFT ,那么 $f(t)$ 被定义为 $f(t) = \frac{t}{2}$
对于经典的荷兰式拍卖,我们可以使用以下方法计算 NFT 价格的下降幅度:
$$ (1 - k)^{t} $$
但是为了实现我们调控 NFT 发行的目标,我们需要插入调整因子,最简单的调整方案是调整 $t$ 值,此处引入 $s_n$ 变量,则 NFT 定价为:
$$ p(t) = p_0 (1 - k)^{t - s_n} $$
与常规的荷兰式拍卖不同,此处的 $p_0$ 不是起拍价而是按计划发行的目标价格,真实的起拍价为 $p_0 (1 - k)^{-s_n}$
此处,我们需要求解 $s_n$ 的表达式。当用户在预期时间内买入 NFT 时,我们认为其购入价格为按计划出售的目标价格 $p_0$ ,即满足:
$$ p_0 (1 - k)^{t - s_n} = p_0 $$
化简,即获得 $t = s_n$ 的结果,注意此时的 $t$ 为预期发行时间,其可以使用 $f^{-1}(n)$ 计算获得。
基于以上推导,我们获得了第 n 个 NFT 的 VRGDA 的价格计算公式:
$$ \mathtt{vrgda_n}(t) = p_0 (1 - k)^{t - f^{-1}(n)} $$
根据此处的预期发行计划的不同(即 $s_n$ 的不同),我们可以设计不同的 VRGDA。
此处出现了 $(1 - k)^{t - f^{-1}(t)}$ 的幂运算,一般来说,我们会使用以下转化使其更加方便实现:
$$ \begin{align} \mathtt{vrgda_n}(t) &= p_0 (1 - k)^{t - f^{-1}(n)} \\ &= p_0 e^{(t - f^{-1}(n)) \cdot ln(1 - k)} \end{align} $$
具体实现代码如下:
constructor(int256 _targetPrice, int256 _priceDecayPercent) {
targetPrice = _targetPrice;
decayConstant = wadLn(1e18 - _priceDecayPercent);
// The decay constant must be negative for VRGDAs to work.
require(decayConstant < 0, "NON_NEGATIVE_DECAY_CONSTANT");
}
function getVRGDAPrice(int256 timeSinceStart, uint256 sold) public view virtual returns (uint256) {
unchecked {
// prettier-ignore
return uint256(wadMul(targetPrice, wadExp(unsafeWadMul(decayConstant,
// Theoretically calling toWadUnsafe with sold can silently overflow but under
// any reasonable circumstance it will never be large enough. We use sold + 1 as
// the VRGDA formula's n param represents the nth token and sold is the n-1th token.
timeSinceStart - getTargetSaleTime(toWadUnsafe(sold + 1))
))));
}
}
此处的 getTargetSaleTime 即 $s_n$ 的计算实现。
线性 VRGDA
线性 VRGDA 适用于计划每日固定释放代币的场景,其目标发行计划函数为 $f(t) = rt$ ,简单计算就可以获得 $s_n = \frac{n}{r}$ 的结论。

第 n 个 NFT 的 VRGDA 的价格计算公式:
$$ \mathtt{linear\_vrgda}(t) = p_0 (1 - k)^{t - \frac{n}{r}} $$
下图展示了当 $n = 2$ 和 $n = 3$ 时的线性 VRGDA 的价格情况:
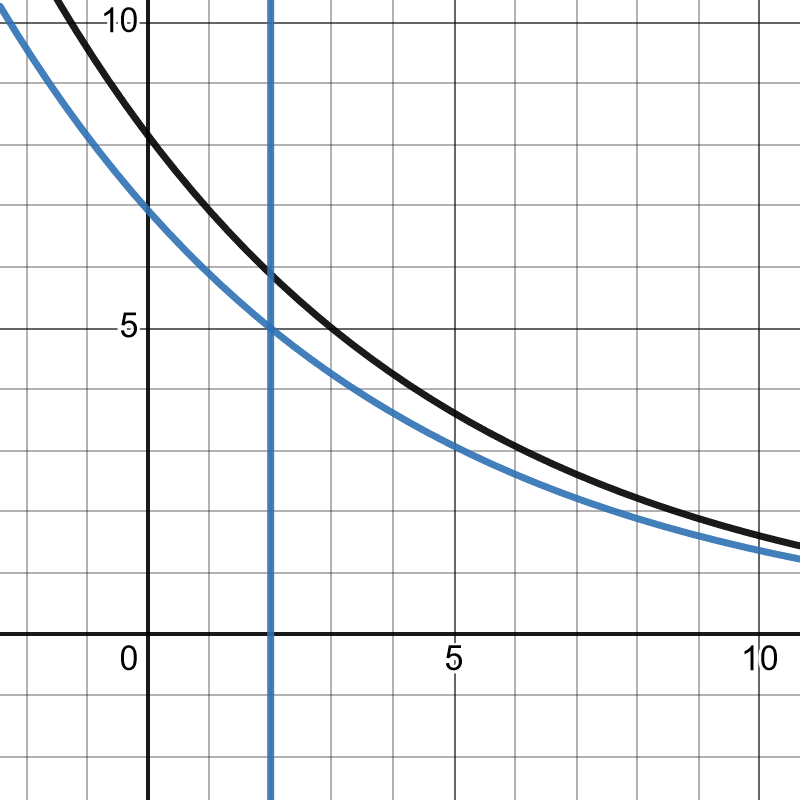
此图也可以通过 此链接 查看
开方 VRGDA
适用于开始以较高速率发行 NFT,然后随着时间的推移更慢地发行 NFT,但永远不会停止的 NFT 计划排放场景,如下图:
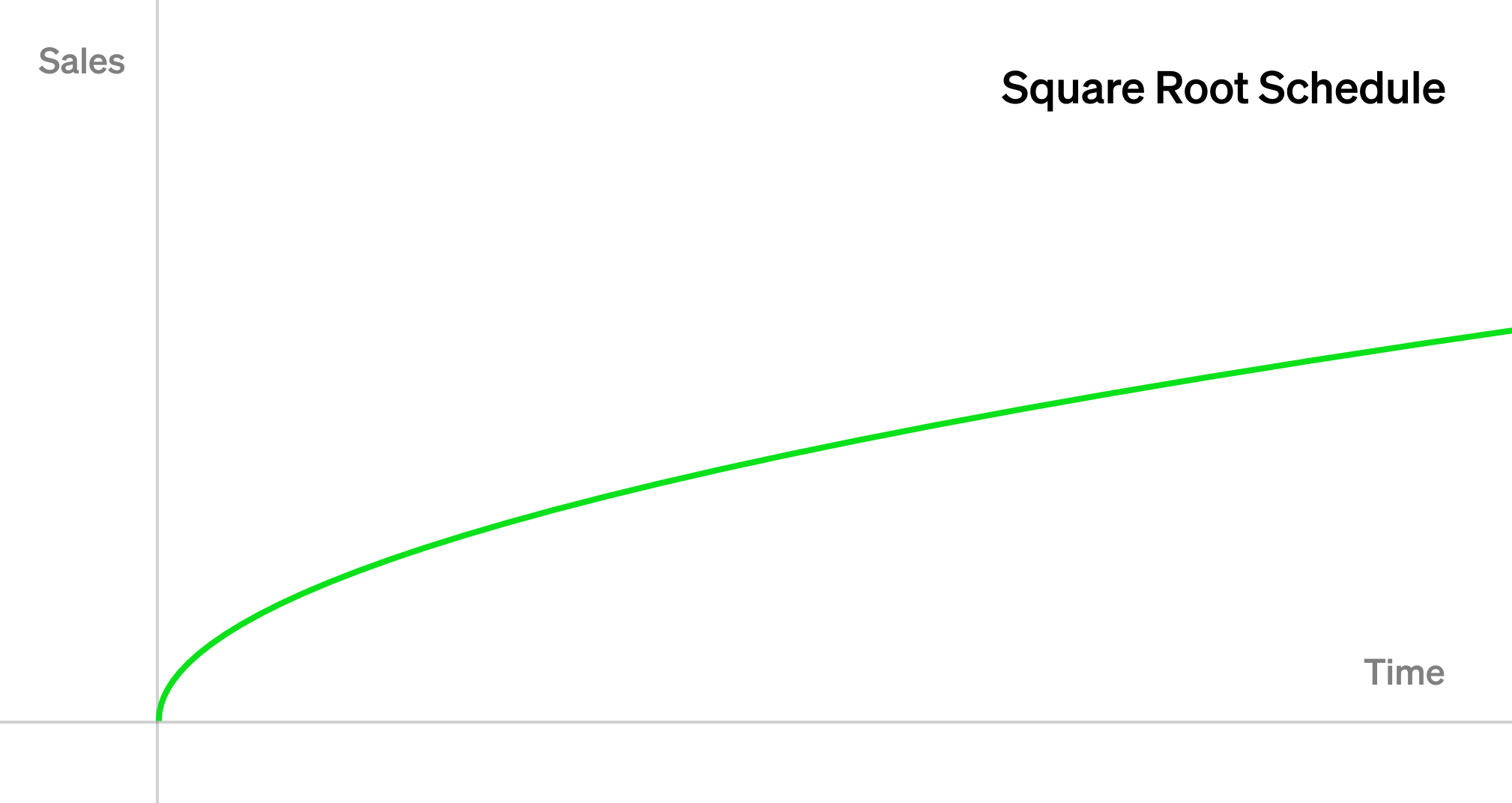
此时,计划发行函数为 $f(t) = \sqrt{t}$ ,此时 $s_n = n^2$ ,那么 VRGDA 的价格计算公式如下:
$$ \mathtt{linear\_vrgda}(t) = p_0 (1 - k)^{t - n^2} $$
其价格图像如下,绿线的参数为 $n = 1$ 而黑线参数为 $n = 2$:
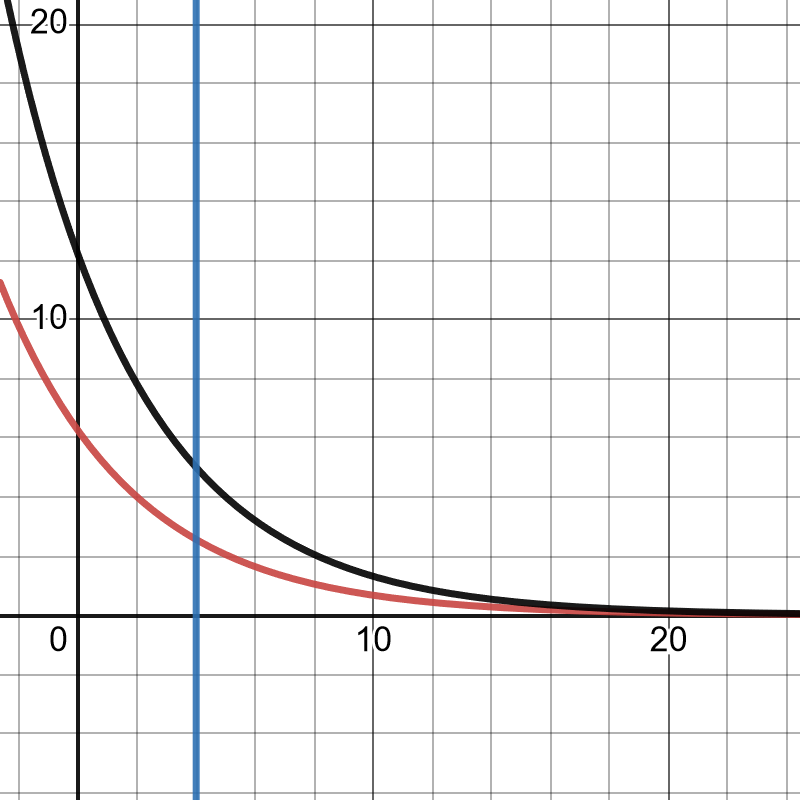
此图也可以通过 此链接 查看
总结
上述介绍的所有拍卖函数其实都是基于离散 GDA 在数学上修正获得。离散 GDA 是为了避免频繁的启动荷兰式拍卖,所以选择直接通过因子 $\alpha^{n}$ 进行起拍价调整,实际上等同于将集合内的各个 NFT 以不同的起拍价进行荷兰式拍卖,避免每一个 NFT 都单独启动一次拍卖。
连续 GDA 实际上用于解决 ERC20 等同质化代币的拍卖,其解决方案为将代币无限细分后,对每一份无限细分后的代币进行拍卖,其价格仍使用荷兰式拍卖确定。由于其连续属性,所以连续 GDA 无法使用 $\alpha^n$ 的方式进行起拍价调整,所以实际上每份代币的价格会随着时间推移逐渐下降。此处由于用户一次性需要购买一定数量的代币,所以我们使用了积分的方案,其积分下限为当前时间而积分上限为当前时间减去用户购买的代币所需要的释放时间。
对于离散 GDA 而言,我们无法通过价格调控 NFT 的铸造情况,所以我们在离散 GDA 内再次引入 $s_n$ 变量以调整荷兰式拍卖过程中的价格下降情况。
但无论使用何种方案,GDA 都属于荷兰式拍卖变体。使用 GDA 容易造成用户倾向于进行长时间等待以获得拍卖的最低价。