概述
本文主要介绍如何在AAVE内进行质押、借贷等基本操作,为读者进一步研究AAVE源代码奠定坚实的基础。
本文要求读者具有以下条件:
- 熟悉以太坊钱包使用
- 拥有一定的
GoerliETH测试网ETH,可前往Goerlin Faucet进行领取
上述条件可以保证读者可以理解本文的大部分内容,由于笔者本人具有较强的技术背景且未来准备编写AAVE智能合约解析系列文章,所以本文给出了部分合约裸交互(即直接与合约函数交互而并不通过网页),理解这一部分内容需要读者了解智能合约开发和cast使用。如果您不是技术人员,可以酌情跳过此部分。考虑到安全性问题,本文提供的裸交互均为eth_call而不涉及真正的交易(需要签名和区块确认的交易)。
本文使用
AAVE V3版本,此版本暂未在以太坊主网部署,在L2网络的详细部署地址可以参考文档
初始准备
前往AAVE DApp官网,连结并授权钱包,点击右上角的齿轮符号,开启Testnet mode。如下图:
然后,进入Faucet页面,铸造一部分Test Assets,建议铸造USDC资产。
存入资产
存入步骤
完成初始测试资产的铸造后,我们返回到Dashboard页面,在Assets to supply栏目内选择USDC资产进行Supply操作,如图:
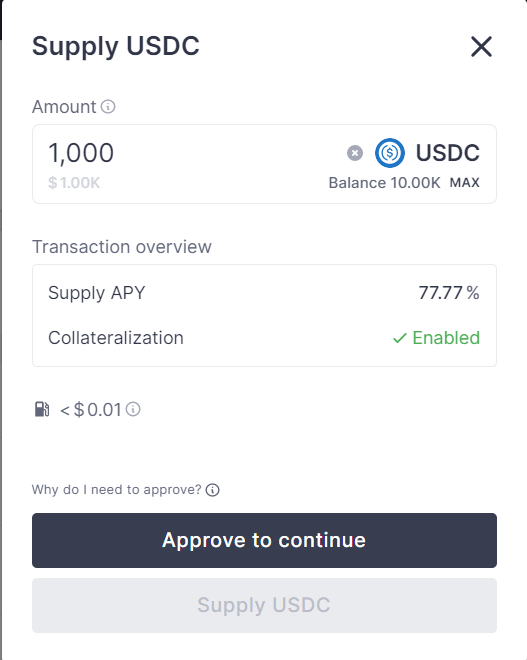
点此查看我的交易
点击Approve to continue按钮,并在钱包内批准交易。值得注意的是,此笔交易完成后,并不以为这我们完成了Supply操作,这仅仅表示我们完成了ERC-20的Approve操作。我们需要再次点击Supply USDC,如图:
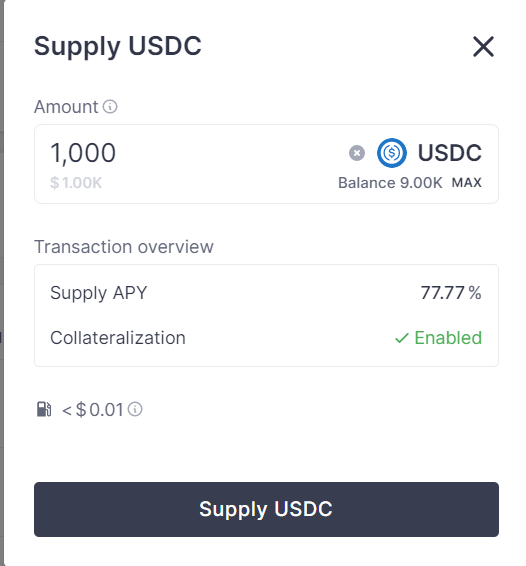
点此查看我的交易
最终,完成后会出现以下对话框:
质押利率计算
由于AAVE属于纯粹的DeFi,所有贷款获得盈利将分配给质押用户,所以我们可以通过以下公式进行计算:
$$ {LR}_t = \bar{R_t}{U_t} $$
$$ \bar{R_t} = \frac{variable\ debt}{total\ debt} * {R_{variable}} + \frac{stable\ debt}{total\ debt} * {R_{stable}} $$
其中,各参数含义如下:
- $\bar{R_t}$ 浮动利率贷款与固定利率贷款的利率加权平均值(以占总贷款数量的比值为权数)
- $U_t$ 流动性资金利用率,即当前流动性池内贷出资产与总资产的比值
上述获得 ${LR}_t$ 实际上属于单利利率,在AAVE内,合约采用了每秒进行一次复利的方法进行计算利率,实际复利利率计算公式如下:
$$Actual\ APY = (1+Theoretical\ APY/secsperyear)^{secsperyear}-1$$
我们上文给出的 $R_t$ 即此处的 $Theoretical\ APY$ ,$secsperyear$ 含义为 每年的秒数,计算一下可以得到此值等于31536000
如果读者具有金融背景,可以将此按秒复利的方法近似于
连续复利,通过 $e ^ {Theoretical\ APY} - 1$ 获得近似值。
事实上,贷款收益并不会完全分配给用户,有少部分的利息收入会被计入风险储备金,此部分比例一般较少,在上文中并没有给出相关参数。
事实上,我们可以通过与AaveProtocolDataProvider合约中的getReserveData函数获得相关数据,具体函数参数和返回值可参考文档。这里以Arbitrum上的DAI资产为例介绍参数获得。
直接前往Arbiscan相关页面操作,在asset内输入DAI的地址0xda10009cbd5d07dd0cecc66161fc93d7c9000da1,我们就可以索引到相关数据,如下图:
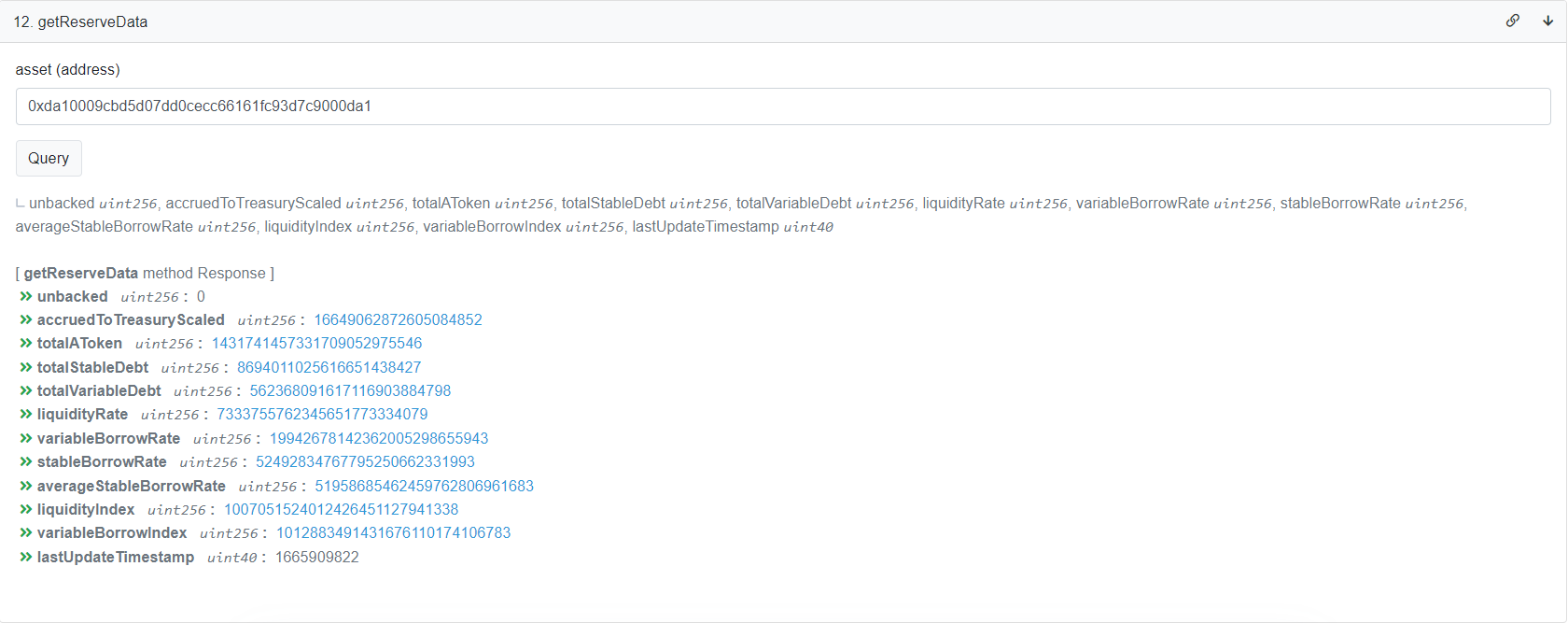
返回的liquidityRate就是我们想要的 ${LR}_t$ ,但由于有限精度小数编码的方法,此处获得的数据需要与 ${10}^{27}$ 相除,即0.00733376。将此数值带入上文给出的实际利率计算公式,结果为
$$ (1 + \frac{0.00733376}{31536000}) ^ {31536000} - 1 = 0.007365$$
实际上,为了减少
gas消耗,AAVE合约采用了二项式近似的计算方法,可参考calculateCompoundedInterest函数。此处为了方便读者计算而直接采用了指数运算的方法。
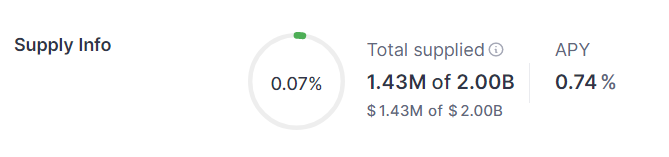
上述数据与 DAPP 详情页显示一致,如下图:
贷出资产
贷款目的
对于很多以不熟悉金融的读者来说,很难理解为什么有人以超额质押的形式贷出资产,而不是选择直接兑换资产。我个人总结了以下几种需要贷款的情形,希望帮助读者理解这一行为:
使用AAVE进行贷款最大的原因是获得流动性。我们首先给出一个传统金融的例子:假如我们个人维护有一个非常完美的由股票构成的资产组合,我们将所有流动性资产投资于此股票组合。但由于各种原因,我们需要一定量的现金,一种最简单的解决流动性问题的方案是直接出售股票组合内的部分资产,但这种行为意味着我们放弃了未来盈利,机会成本较高。另一种可靠的解决方案是通过券商进行股票的质押换取现金,待未来有了流动性资产后回购股票。通过质押回购股票的方式,我们即没有放弃资产组合,但也获得了流动性。这种交易被称为融资交易(与下文介绍的融券交易相对)。但质押回购股票要求投资者必须为合格投资者,门槛非常高。
使用AAVE的贷款功能可以很好的解决上述问题。我们仍假设维护有一个良好的资产组合,但这些组合由很多以太坊内的ERC-20代币构成且盈利稳定。我们遇到流动性危机时,仅需要将资产储蓄在AAVE的流动性池内,然后贷出稳定币就可以非常快速的解决流动性问题。且我们可以无许可地使用这套金融系统。
上述情况的另一个选择是使用
MarkDAO通过铸造DAI解决问题,此种方式似乎更加常见,这也是为什么MarkDAO是目前以太坊内总锁仓量最大的DeFi的原因
使用AAVE进行贷款的第二个原因是可以进行投机。在传统金融中,尤其在没有做空机制的A股内,当我们需要做空一只股票,除了期货这类可做空的衍生品外,我们另一种途径是融券交易,即我们向券商质押一部分流动性较好的资产,然后券商会贷出一部分自己持有的股票。我们可以直接在股票市场上卖出这部分贷出的股票,获得现金。当股票价格下跌后,我们再买入股票归还给券商,并拿回质押品。这种融券交易实现了做空股票的功能。与上文介绍的融资交易相同,此交易也需要投资者具有合格投资者地位,门槛非常高。
在AAVE中,我们可以通过把一部分价值较为稳定的资产质押到流动性池内,贷出目标资产,获得目标资产后,我们直接卖出目标资产获得现金。等到目标资产价格下跌到一定水平后,我们使用之前卖出资产获得的现金购买目标资产,偿还贷款,解除质押。显然,这种方式更加优雅且有效。
如果读者想获得更多传统金融方面的知识,我建议读者可以尝试考取
证券从业资格证,此证书可以较为容易地考取,并帮助读者获得金融领域的基础知识
综上所述,我个人认为AAVE不应该被称为Web3银行,而应该被称为Web3融资融券机构,这更符合AAVE的功能定位。银行最大的运行特点是借长贷短,但AAVE并没有设计锁仓机制实现借长的目的,在贷出资产方面也没有要求用户需要在指定期限内归还贷款,所以AAVE被称为Web3银行是一个非常不好的类比。
贷款参数
正如在现实世界内的贷款,我们需要认真研究贷款利率、当前资产可贷出的总金额等属性。但在AAVE内,由于其用户进行清算的属性,我们需要研究更多的金融属性。在此处,我们假设将USDC全部用于质押以贷出USDT。
首先,我们应该点击Assets to borrow栏目内的Details按钮以查询作为抵押品的USDC的相关属性。当然,读者可以通过直接点击此链接直接访问。如图:
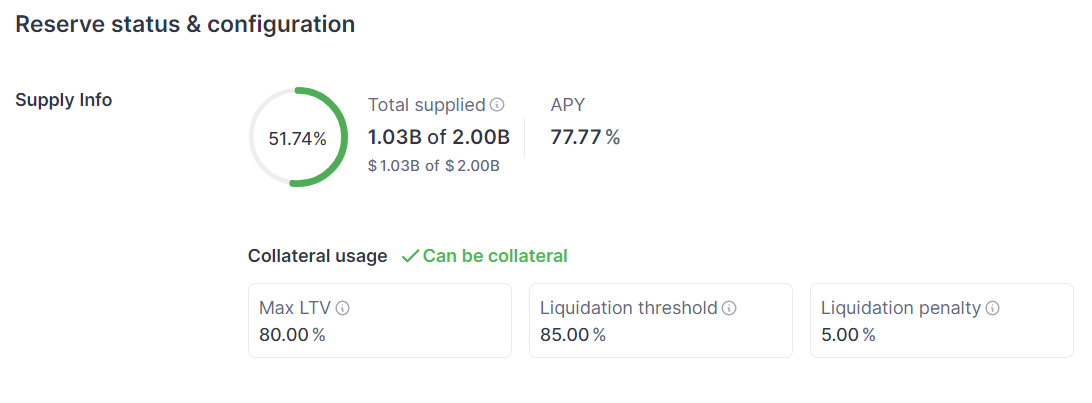
其中,各参数含义如下:
APY年利率Max LTV贷出资产价值与质押品价值的最大比值Liquidation threshold清算阈值,如果抵押资产与贷出资产的价值比率低于此值,会触发清算Liquidation penalty资产被清算时,清算人使用被清算人贷出资产购买抵押品的折扣
在前文中,我们存入了 1000 USDC 资产,根据Max LTV计算出,我们最多可以贷出 800 美元的其他资产。由于USDC的APY过高,我目前持有1000.21 USDC,假如兑换USDT,根据Max LTV计算得到我可以借出最多800.168 USDT,查看USDT Details页面,数值恰好相符。
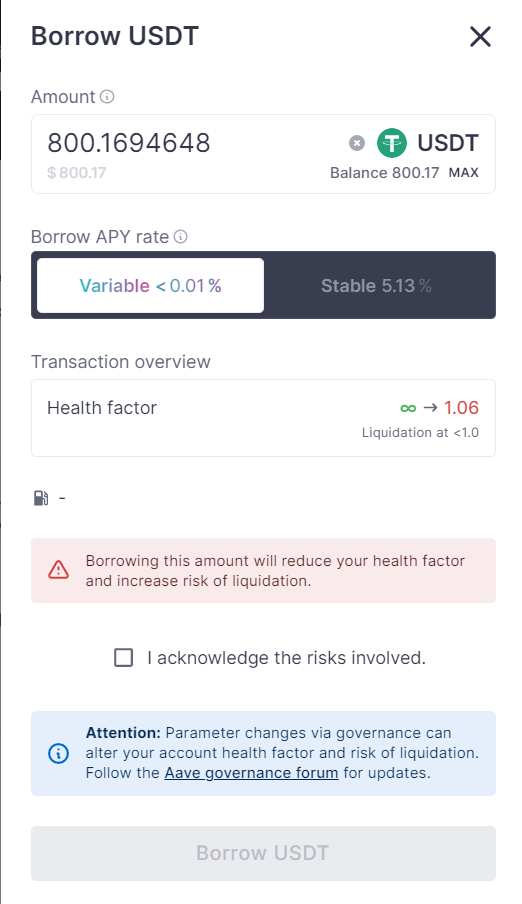
接下来,我们计算Health factor数值,此数值一旦低于1,就会触发清算程序。此数值的计算方法为清算阈值(Liquidation threshold) / 贷出资产价值与质押品价值比值。在此处,我们可以计算出贷出资产价值与质押品价值比值为80 %(此处我们选择全部贷出,故而数值等同于Max LTV),而USDC的清算阈值为85 %,我们可以通过85% / 80%,结果正好为1.06。
一个更加权威的且适合于多种资产联合质押情况下Health factor计算公式如下:
$$H_f = \frac{\sum({Collateral_i\ in\ ETH} \times {Liquidation\ Threshold}_i)}{Total\ Borrows\ in\ ETH}$$
各参数含义如下:
- $H_f$ 健康因子,即
Health factor - $Collateral_i\ in\ ETH$ 资产 $i$ 以
ETH计价的价值 - ${Liquidation\ Threshold}_i$ 资产 $i$ 对应的清算阈值
- $Total\ Borrows$ 用户借出的总资产价值(以
ETH计价)
上述公式可以计算以资产组合为抵押贷出一系列资产的Health factor。
在上文给出的参数中,较难理解的是Liquidation penalty的含义,我们通过一个例子向大家介绍此参数的含义。在现实世界,当我们无法支付贷款,那么银行会收走我们的抵押品进行拍卖以收回贷款。在AAVE内流程类似,当用户无法偿还贷款时,其抵押品会被出售,但为了激励清算人购买抵押品,抵押品会折价一定比例,此比例即Liquidation penalty。当然,这部分资产需要贷款人支付,相当于清算手续费。
清算人只能使用被清算人的贷出资产类别进行清算购买
清算资产的具体规则如下:
- 当贷款的
Health factor小于 1 时,清算启动,但此时清算人只能最多清算 50% 的贷款 - 当贷款的
Health factor小于 0.95 时,清算人可以清算贷款人 100% 的贷款
清算人清算后会获得质押物的aToken。
总结来说,清算人单次清算的贷款金额可以通过以下公式计算:
$$ debtToCover = \begin{cases} (userStableDebt + userVariableDebt) \times 50\% &\text{if } 0.95 < H_f < 1 \\ (userStableDebt + userVariableDebt) \times 100\% &\text{if } H_f \leq 0.95\ \end{cases} $$
其中,各参数含义如下:
- $debtToCover$ 代表可偿还贷款金额
- $userStableDebt$ 代表被清算人的固定利率贷款金额
- $userVariableDebt$ 代表被清算人的浮动利率贷款金额
- $H_f$ 健康因子,即
Health factor
最大可清算质押品数量可以通过以下公式计算:
$$ maxAmountOfCollateralToLiquidate = \frac{debtAssetPrice \times debtToCover \times liquidationBonus}{collateralPrice} $$
其中,各参数含义如下:
- $maxAmountOfCollateralToLiquidate$ 最大可清算质押品数量
- $debtAssetPrice$ 贷出资产的价值(以ETH计)
- $debtToCover$ 可偿还贷款金额
- $liquidationBonus$ 等于
1 - Liquidation penalty - $collateralPrice$ 质押资产价值(以ETH计)
在下文中,我们不会使用此公式,但如果读者意图开发清算MEV机器人需要使用此公式计算
清算者在清算过程中需要清偿贷款,清偿所需要的输入的资产如下:
$$ debtLiquidate = debtAssetPrice \times debtToCover \times liquidationBonus $$
经过简单的数学推导,我们可以得到清算人在清算过程中获得清算奖励:
$$ maxCollateralBonus = maxAmountOfCollateralToLiquidate \times (1- liquidationBonus) \times collateralPrice $$
我们看一笔发生在真实世界的交易,更加详细的交易调用可以参考此网站。简单来说,质押者在过去以383.4730870573113 REN以及其他资产作为质押品贷出了114.5628671559096 DAI。但目前,这笔交易已经到达清算阶段。上面给出的交易正是此交易的清算交易之一。清算人决定质押品内所有的REN代币,总计383.4730870573113。由于被清算人贷出了DAI,所以清算人需要支付DAI作为代币,且仅需要支付383.4730870573113 * (1 - 0.075) REN的DAI。
此处
0.075即Liquidation penalty,这部分费用由被清算人支付
查阅交易调用记录,我们可以得到在交易发生时,REN、DAI与ETH的兑换比率如下:
1 REN = 94627327009678 wei ETH
1 DAI = 752403700000000 wei ETH
我们计算清算人所需要支付的DAI,计算公式如下:
383.4730870573113 * 94627327009678 / 752403700000000 * (1 - 0.075)
计算结果为44.61103223941377,基本与交易输入的44.86338878495268 DAI。
上述误差可能来自浮点数计算以及结算手续费等问题。如果读者想更加详细了解此部分或者构造清算机器人,请一定阅读AAVE liquidations
读者可以在eigenphi网站内找到更多清算实例。如下图:
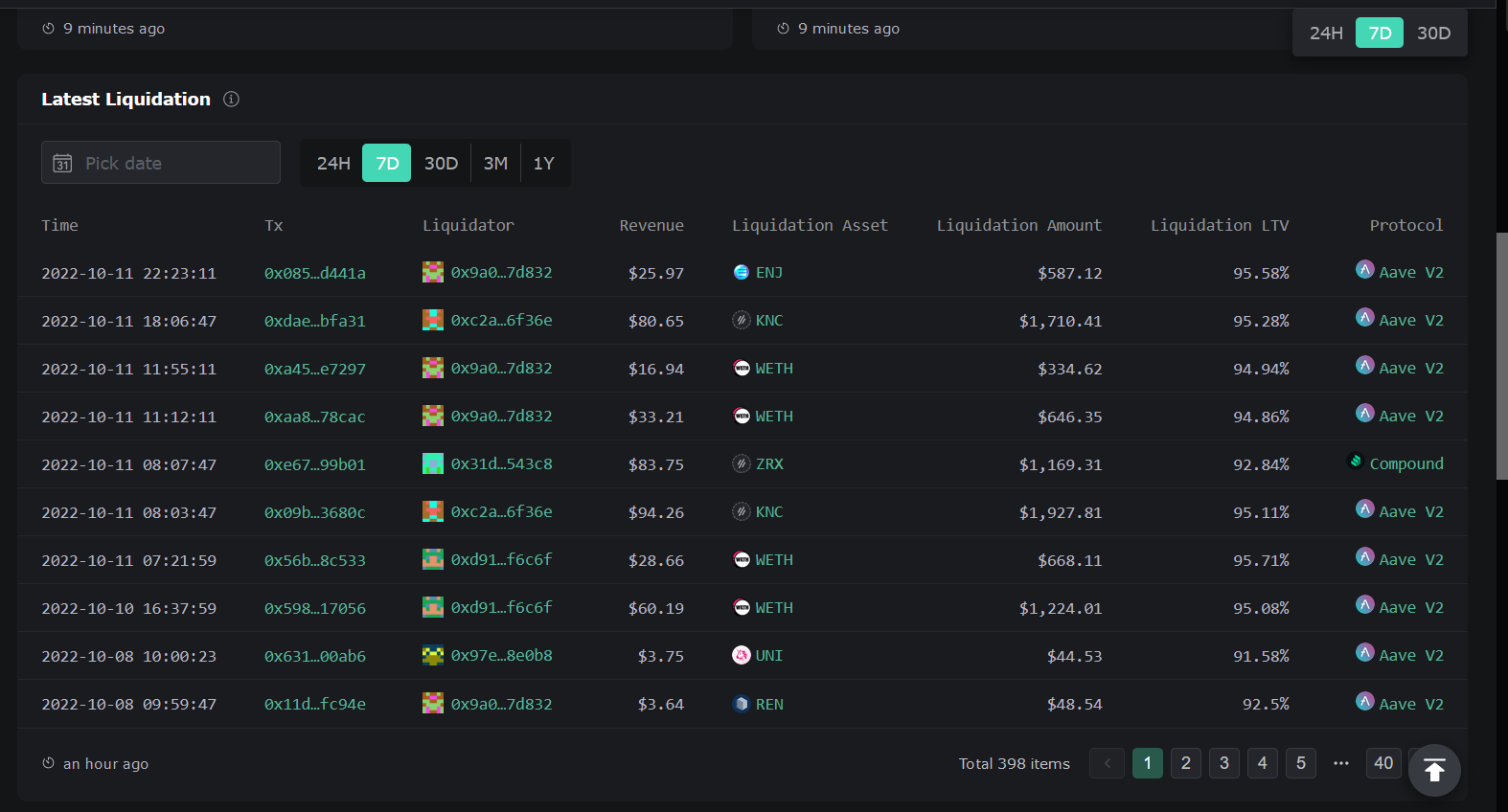
但值得注意的是,此网站展示的结算过程较为会计化和复杂化,可能很难理解具体的清算流程。如下图:
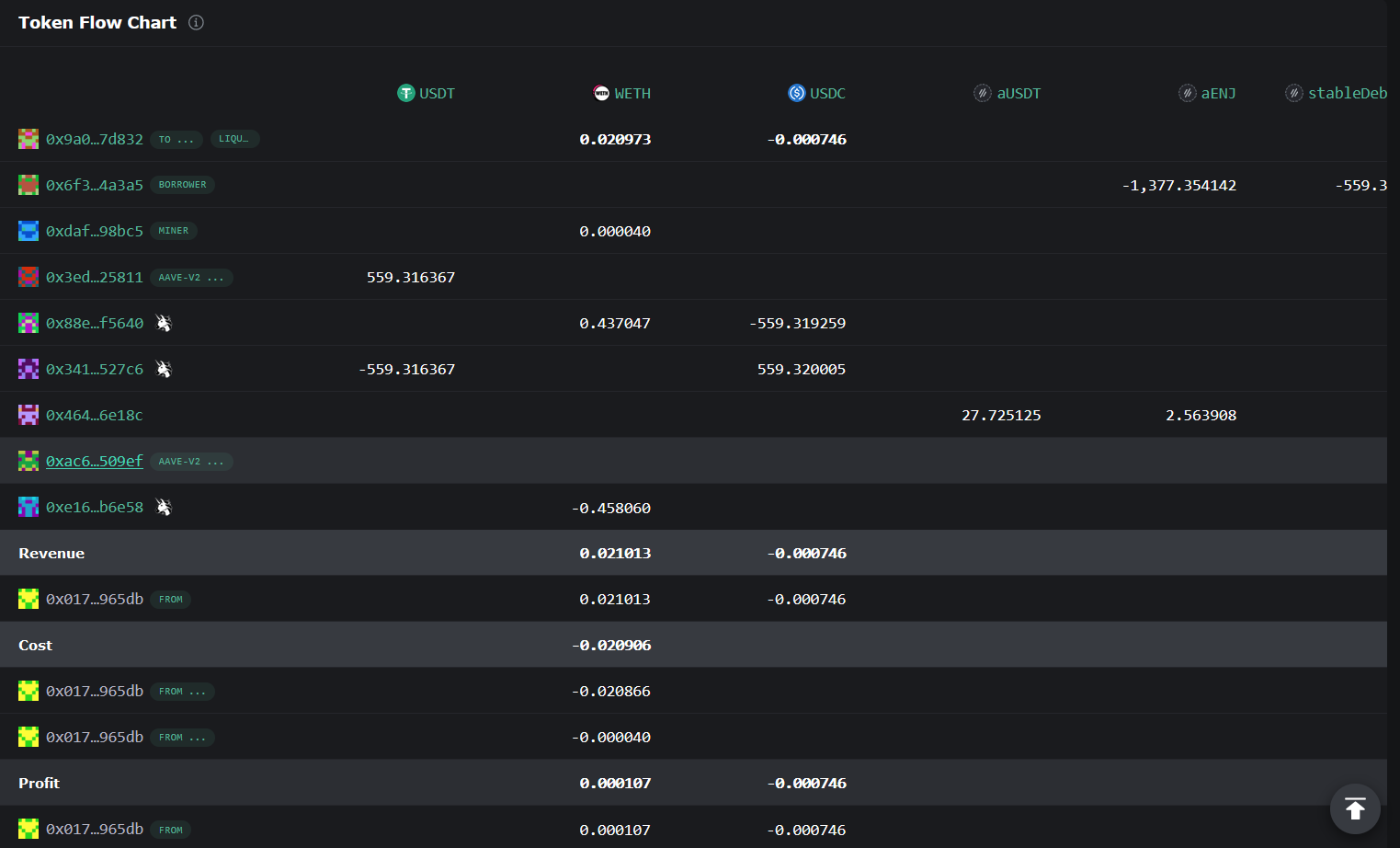
这是因为清算人在清算时往往大量使用uniswap等工具进行代币兑换,但此部分展示时并没有给出详细的交易执行顺序而仅仅给出交易运行结束后的代币流向,一个更好的理解清算过程的方法是使用Etherscan,如下图:

读者可以通过在eigenphi交易详情页的最上方的按钮直接跳转到Etherscan,如下图:

如果您是一位以太坊技术人员,更希望了解交易的本质,我建议您通过此网站查询清算交易的详细的函数调用情况。
我们在此处也给出不通过AAVE网页获得这些参数的方法。如果您不是技术人员,请不要阅读此部分。
在此处我们使用Arbitrum网络上的DAI流动性池作为案例,页面上的参数如图:
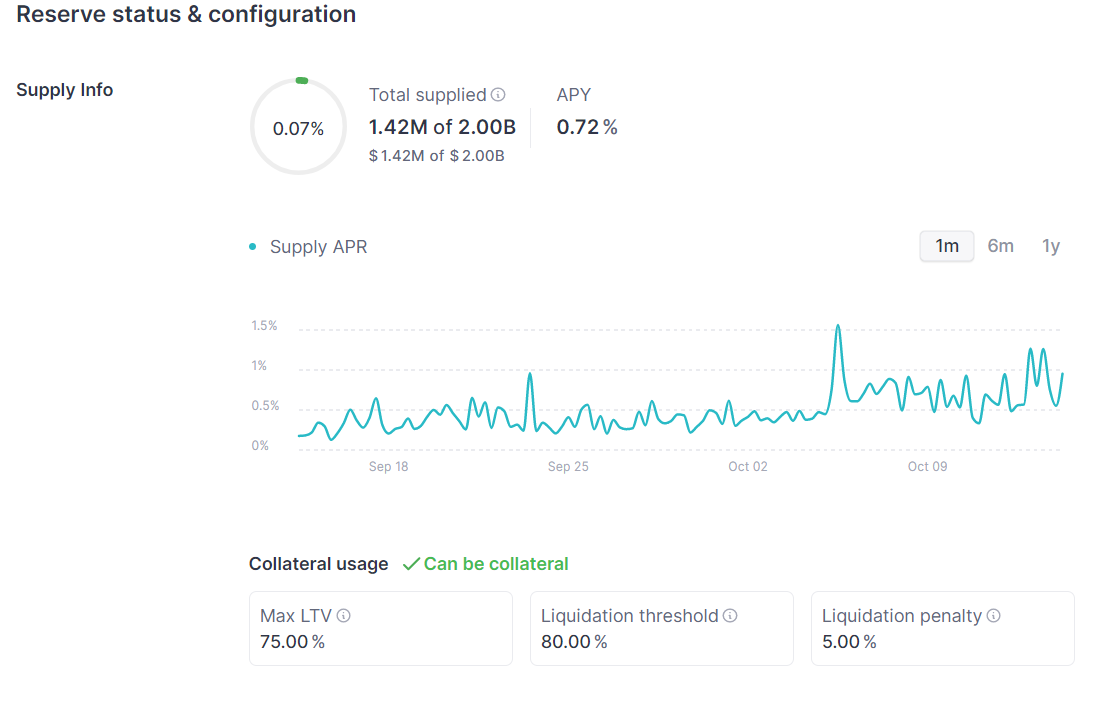
我们可以通过Pool合约的getReserveData函数获得压缩后的流动性池配置,使用以下命令获得相关数据:
cast call 0x794a61358D6845594F94dc1DB02A252b5b4814aD "getReserveData(address)(uint256)" 0xda10009cbd5d07dd0cecc66161fc93d7c9000da1 --rpc-url https://rpc.ankr.com/arbitrum
cast命令为Foundry框架携带的,具体可参考Foundry教程:编写测试部署ERC-20代币智能合约。
获得的结果为379853576081034459698860574047498960397610237566284,此uint256数字中是由流动性池各个设置压缩产生的,我们在此处目标是提取LTV、Liquidation threshold和Liquidation penalty参数。读者可以打开任一程序语言的交互模式(我个人使用的是Python),键入以下命令:
>>> rep = 379853576081034459698860574047498960397610237566284
>>> rep & ~ 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF0000
7500
>>> (rep & ~ 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF0000FFFF) >> 16
8000
>>> (rep & ~ 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF0000FFFFFFFF) >> 32
10500
命令最开始的
>>>均为命令提示符,不需要输入
上述输出依次为LTV、Liquidation threshold和Liquidation bonus。其中Liquidation bonus相当于Liquidation penalty + 1。由于以太坊不支持小数,所以上文的值其实都是设置值乘以10000的结果,换算后LTV为0.75(75%),Liquidation threshold为0.80(80%),Liquidation bonus为1.05(105%)。通过Liquidation bonus可以解算出Liquidation penalty为5%,这些数据均正确。
我们会在以后解析AAVE合约时说明上述位运算的原理。如果读者十分好奇,可以首先参考此文档获得各个二进制位与流动性池参数设置的对应关系可以参考。然后,读者可以直接阅读此合约。
贷款利率计算
此节主要关注于贷款利率的计算方面。在传统金融中,利率往往通过中央银行给出基准,商业银行在此利率基准上根据资金成本和风险等机制调整利率,较为详细的定价机制可以参考下图:
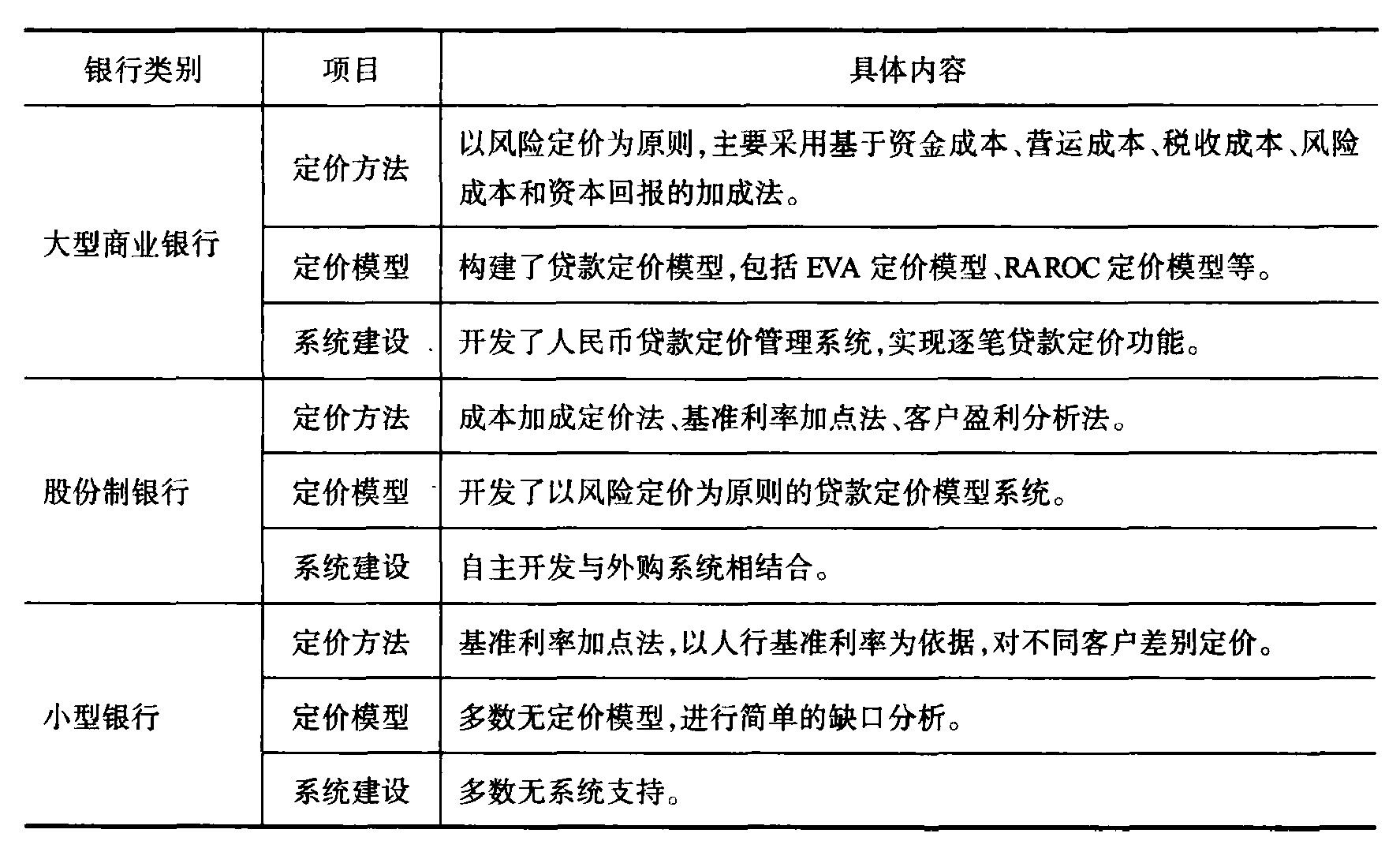
上图来自张建波,文竹.利率市场化改革与商业银行定价能力研究[J].金融监管研究,2012,(10):1-13.
如果读者对此感兴趣,可以参考《商业银行产品定价理论综述》等论文。
但与银行的定价方式不同,在AAVE内,我们通过流动性池实现借贷等功能,利率需要尽可能调整借贷比例以实现流动性池的稳定。为了尽可能实现这一目的,AAVE设计了一个二阶段的利率曲线,具体图像如下:
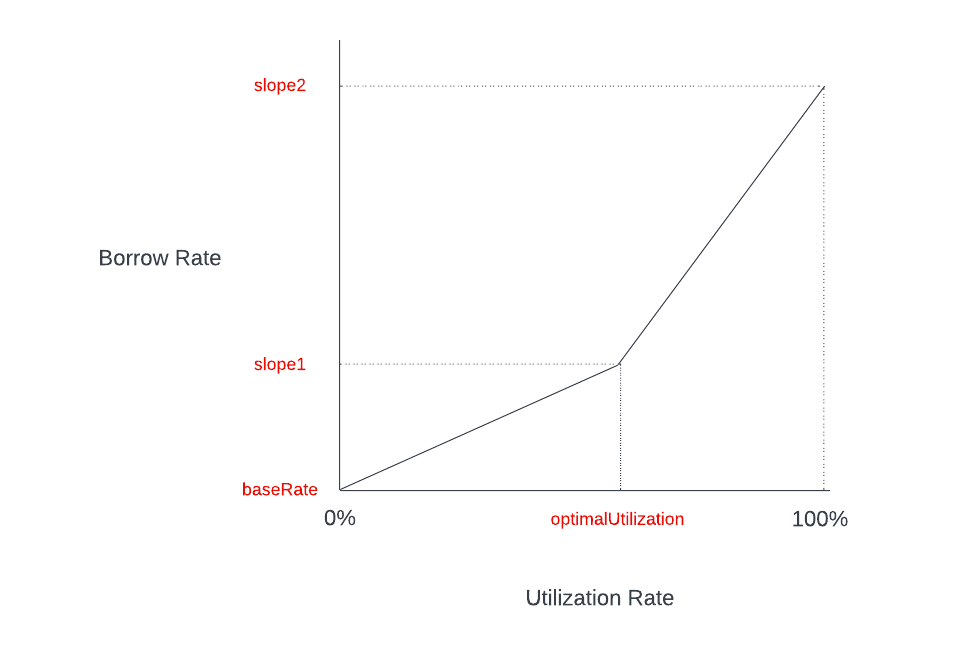
在达成流动性池最佳利用率Optimal后,借贷利率会迅速上升以避免流动性枯竭。
上面的描述都是定性的,接下来我们进行定量化的分析。为了增强本文的实战性,我们以AAVE V3在Arbitrum网络上的DAI流动性池作为分析对象。
在本文编写时,
AAVE V3暂未部署到以太坊主网上,而仅仅部署在L2网络上。
利用率获取
正如上文所说,在资金利用率 $U$ 在Optimal之前与之后是两种不同的情况,我们首先计算 $U$ ,计算 $U$ 的公式如下:
$$ U = \frac{Total\ borrowed}{Total\ supplied}$$
其中,参数含义如下:
Total borrowed该资产总借出数量Total supplied该资产总存入数量
这些变量的近似值都可以在资产详情页内获得,如下图:
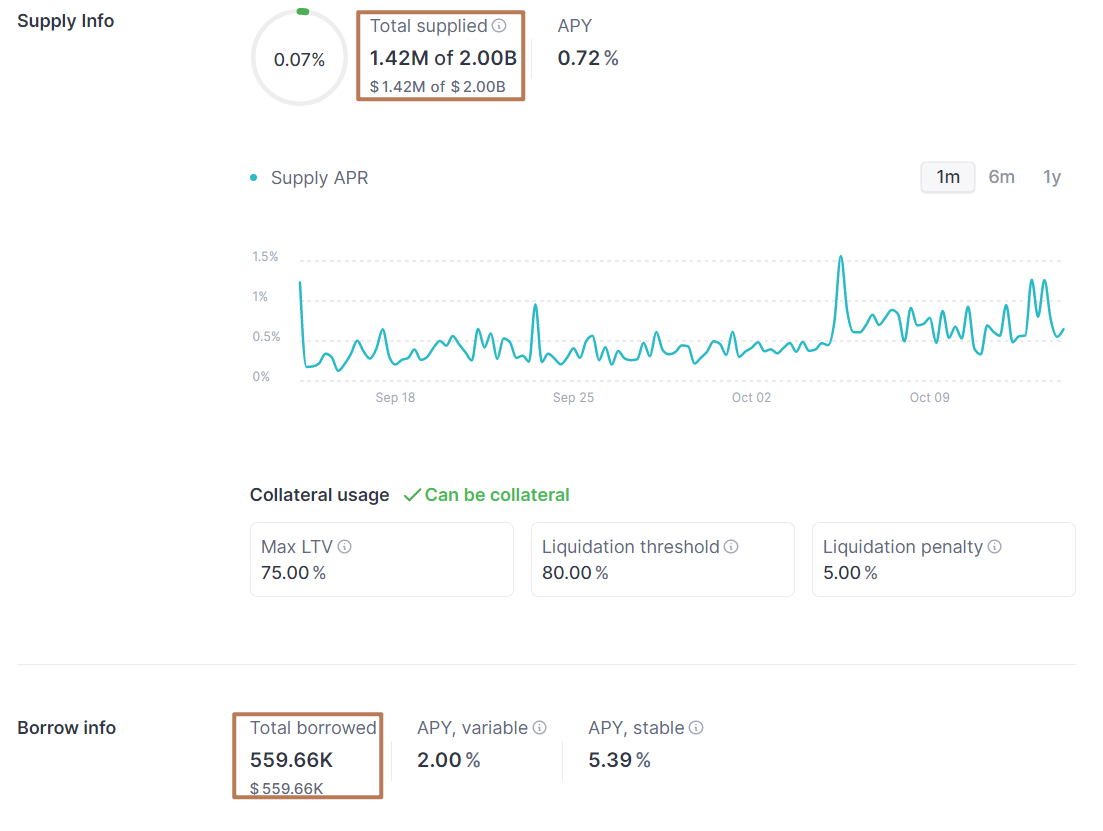
计算得到的结果为39.41%,与页面给出的数据类似:
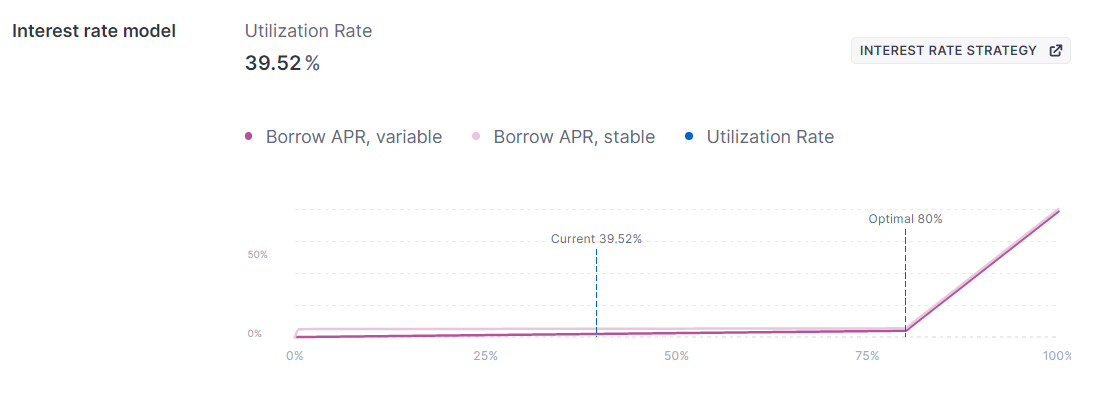
此结果误差原因在于页面给出的贷出、存入资产数据精度不足,为了获得更加精确的数据,我们可以通过与合约进行交互。查询文档,我们可以发现AaveProtocolDataProvider合约内存在getATokenTotalSupply和getTotalDebt(address)函数。
我们可以通过以下命令获得AToken总量,正如上文所述,用户存入代币后获得AToken,所以此处给出的数据相等于用户存储资产总量。
cast call 0x69FA688f1Dc47d4B5d8029D5a35FB7a548310654 "getATokenTotalSupply(address)(uint256)" 0xda10009cbd5d07dd0cecc66161fc93d7c9000da1 --rpc-url https://rpc.ankr.com/arbitrum
0xda10009cbd5d07dd0cecc66161fc93d7c9000da1是Arbitrum网络上的DAI代币地址
以上命令的返回值为1411417181377440330599766,实际等同于1411417.1813774402(18位精度)。
在智能合约内表示小数最简单的方法就是直接使用整数,并通过精度指定小数点的位置。将整数于精度相除即可获得结果。我们可以将
1411417181377440330599766与 $10^{18}$ 相除即可获得小数。
我们通过以下命令获得总借出量,命令如下:
cast call 0x69FA688f1Dc47d4B5d8029D5a35FB7a548310654 "getTotalDebt(address)(uint256)" 0xda10009cbd5d07dd0cecc66161fc93d7c9000da1 --rpc-url https://rpc.ankr.com/arbitrum
返回值为559994183809004825277047,实际相当于559994.1838090048
将上述结果直接相除,获得 $U = 39.6760% $
此值与页面显示的误差已经差别很少,误差可能来自智能合约计算除法时的误差。我们建议在后文使用此数值进行利率计算
浮动利率计算
在具体利率计算中,浮动利率计算较为简单,而固定利率计算较为复杂且依赖于浮动利率计算,所有我们首先分析浮动利率的计算公式,而后分析固定利率计算公式。
我们分析浮动利率确定公式,首先给出流动性利用率 $U < U_{optimal}$ 的情况,具体计算公式如下:
$$R_t = R_0 + \frac{U_t}{U_{optimal}} \times R_{slope1}$$
各参数含义如下:
- $R_t$ 当前利用率 $U_t$ 下的贷款利率
- $R_0$ 初始利率
- $U_t$ 当前流动性池利用率
- $U_{optimal}$ 最佳利用率
- $R_{slope1}$ 预设参数
在 $U > U_{optimal}$ 的情况下,计算公式如下:
$$R_t = R_0 + R_{slope1} + \frac{U_t-U_{optimal}}{1-U_{optimal}} \times R_{slope2}$$
其中,$R_{slope2}$ 为预设参数
接下来,我们介绍各个参数的获取方法:
首先打开流动性池详情页,将页面滚动到最下方,点击Interest rate model框内的INTEREST RATE STRATEGY按钮,如下图:
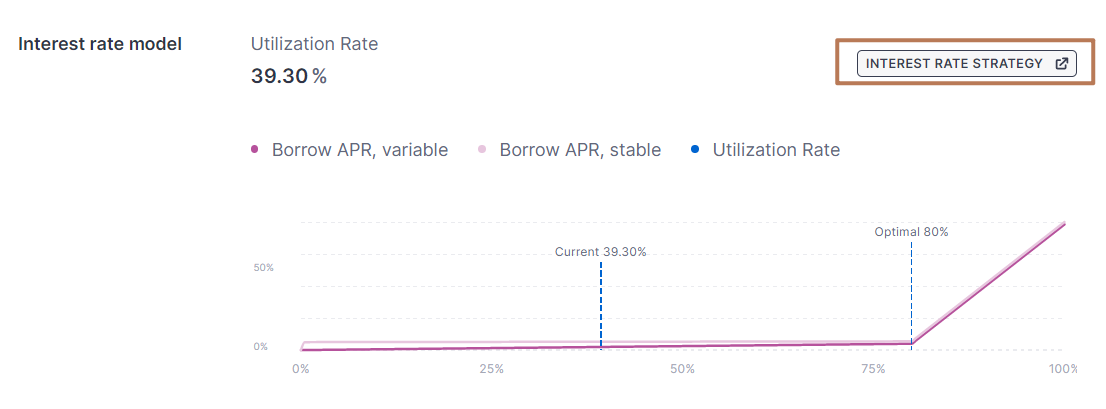
点击后会跳转到Arbiscan网站,点击Contract内的Read Contract,如下图:
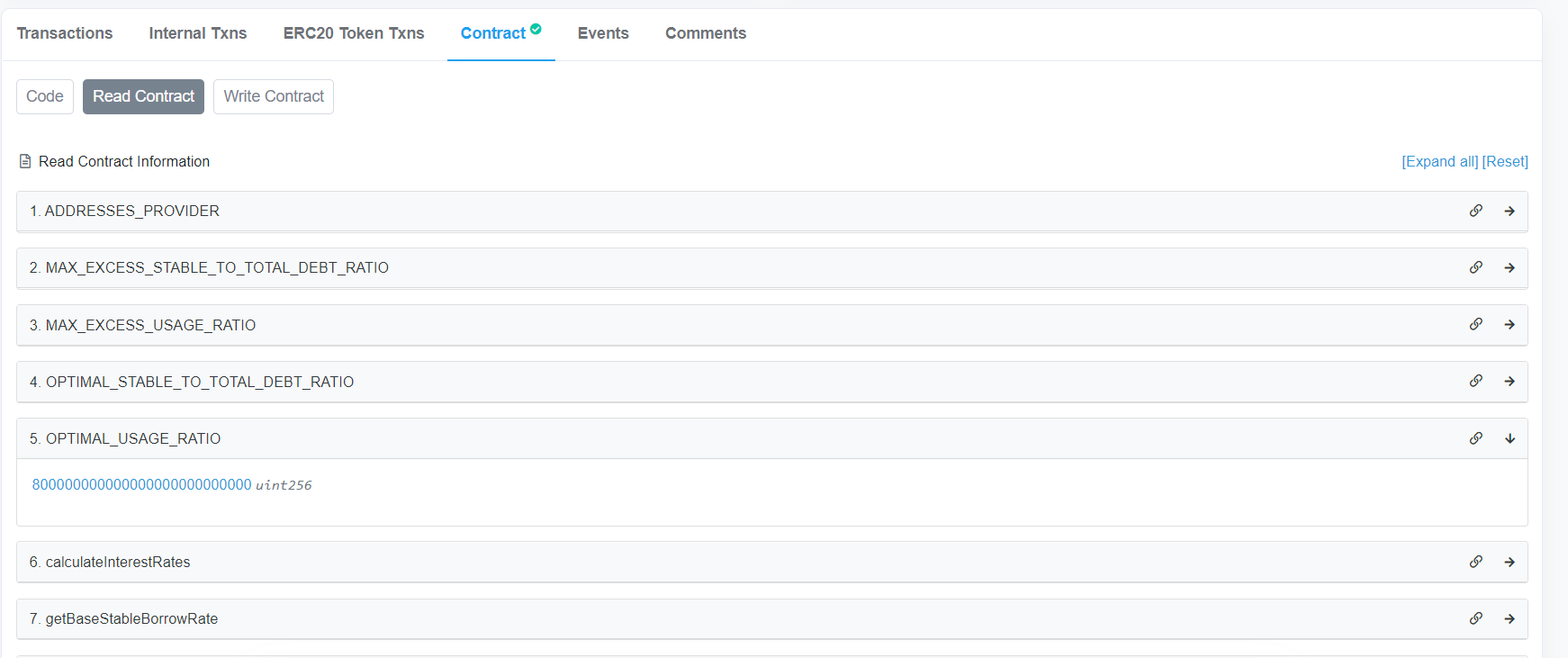
我们可以在此页面内自由参考各个参数,对应关系如下:
OPTIMAL_USAGE_RATIO即最佳利用率 $U_{optimal}$ ,注意需要将返回值除以 $10^{27}$ (该数值被称为RAY,后文所有利率参数均需要除以此值), 数值为0.80getBaseVariableBorrowRate即 $R_0$ ,初始化利率,数值为0getVariableRateSlope1即 $R_{slope1}$ ,数值为0.04getVariableRateSlope2即 $R_{slope2}$ ,数值为0.75
上述计算的结果仅为单利利率,实际的复利利率计算公式参考上文
综合以上数据,我们计算一下当前DAI的利率,其中 $U_t = 0.3929 $ (该数值直接通过合约数据算出,比页面显示数据更加精确)。
注意由于我个人写文章时横跨了两天,此处给出的数据与上文图片给出数据不符是正常的。此处的 $U_t$ 是我根据写作时的最新数据计算出来的,获取方法为合约交互。
首先我们计算 $R_t$ 将数据代入后,结果如下:
$$0 + \frac{0.3929}{80\%} \times 0.04 = 0.019645$$
这与此时页面显示的variable APY是一致的,如下图:
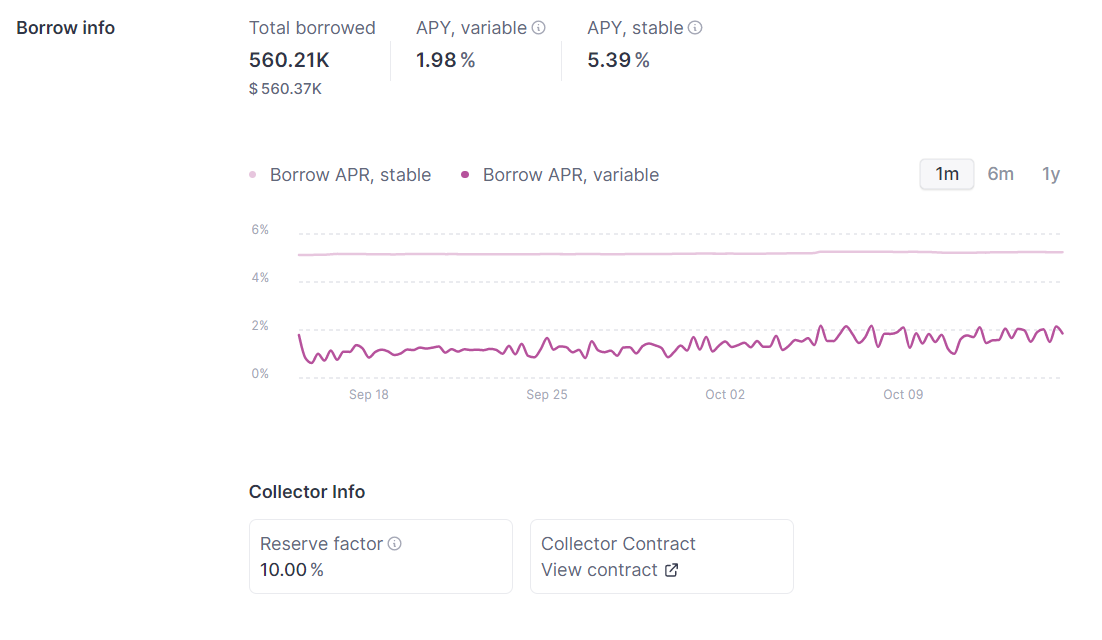
读者可以自行验算当 $U > U_{optimal}$ 情况下的APY在于曲线数值进行核对,我们此处不再给出计算过程。
固定利率计算
上文给出了浮动利率的计算,我们下文将给出固定利率的计算方法。首先我们需要明确一个观点,即固定利率对于流动性池而言风险更高,固定利率不随流动性池进行波动,导致无法对其进行调控,这会造成极大的风险,所以固定利率应该更高以弥补风险溢价。
关于固定利率的计算,在
AAVE的治理论坛中有着一段讨论。大意为,过于激进的稳定利率不能吸引新的流动性,这抑制了协议的增长,并带来更多的用户体验开销(由于利用率高,提取流动性更困难)。
注意此处给出的固定利率计算仅适用于
AAVE V3版本,而目前仍常用的AAVE V2版本固定利率确定依赖于预言机。
为了尽可能减轻固定利率的风险,aave合约引入了最佳固定利率负债总负债比率常数($O_{ratio}$)进行计算。与 $U$ 类似,当流动性池的固定利率负债总负债比率常数($ratio$)大于 $O_{ratio}$ ,我们需要进一步提高利率。
固定利率的基础利率计算公式如下:
$$ R_{base} = \begin{cases} R_0 + \frac{U_t}{U_{optimal}} \times R_{slope1} &\text{if } U < U_{optimal} \\ R_0 + R_{slope1} + \frac{U_t-U_{optimal}}{1-U_{optimal}} \times R_{slope2} &\text{if } U \geq U_{optimal} \end{cases} $$
当获得基础利率 $R_{base}$ 后,我们考虑 最佳固定利率负债总负债比率常数 $O_{ratio}$ 的影响,公式如下:
$$ R_t = \begin{cases} R_{base} &\text{if } ratio < O_{ratio} \\ R_{base} + \frac{ratio - O_{ratio}}{1 - O_{ratio}} \times offset &\text{if } ratio \geq O_{ratio} \end{cases} $$
其中,各参数可通过与合约交互获得,对应如下:
- $ratio$ 固定利率负债与总负债之比,获取方法稍后给出
- $O_{ratio}$ 最佳比例,通过
OPTIMAL_STABLE_TO_TOTAL_DEBT_RATIO获得 - $offset$ 标准偏差,通过
getStableRateExcessOffset获得
由于
AAVE V3白皮书与文档在固定利率计算方面给出的公式语焉不详,此处公式直接参考了DefaultReserveInterestRateStrategy 合约
获得 $ratio$ 的方法较为复杂,我们需要进行合约交互。查询文档发现,获得此数据需要与AaveProtocolDataProvider合约交互通过getReserveData获得相关数据,具体函数参数和返回值可参考文档。在Arbitrum网络上,此合约地址为0x69FA688f1Dc47d4B5d8029D5a35FB7a548310654。(部署地址可在此页获得)。
直接前往Arbiscan相关页面操作,在asset内输入DAI的地址0xda10009cbd5d07dd0cecc66161fc93d7c9000da1,我们就可以索引到相关数据,如下图:
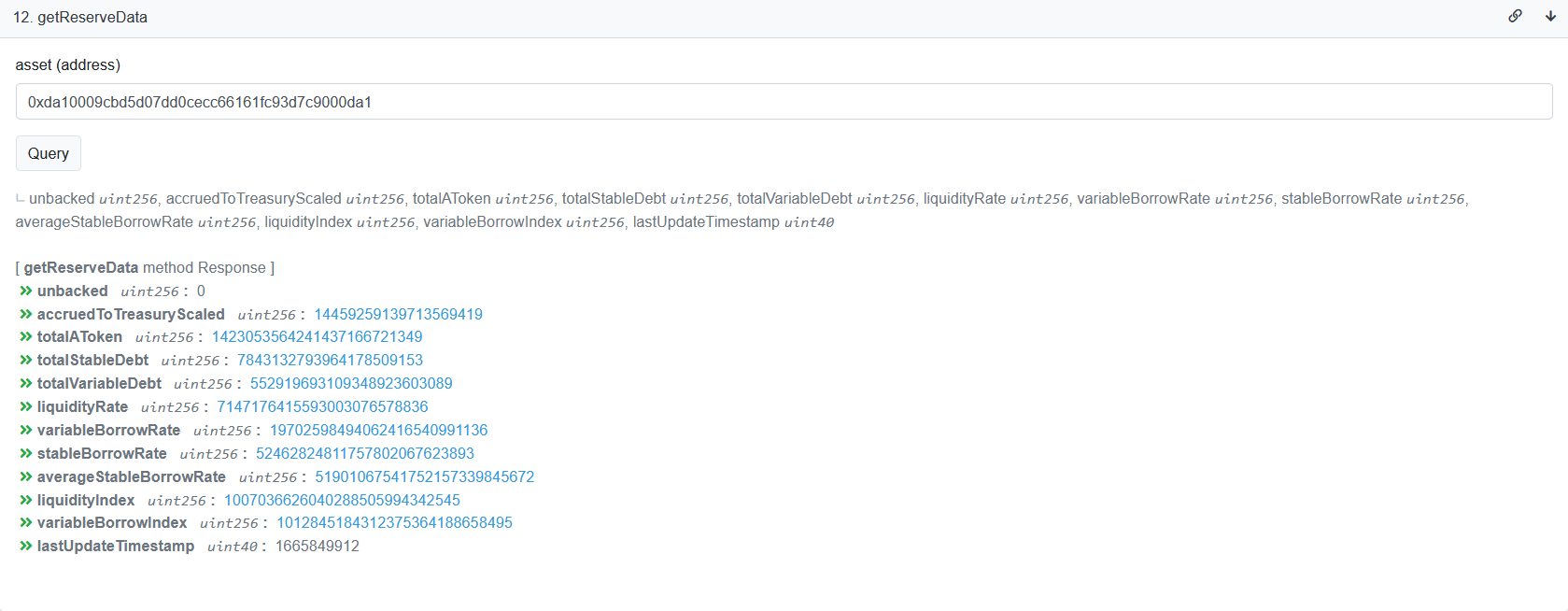
可以通过
cast call 0x69FA688f1Dc47d4B5d8029D5a35FB7a548310654 "getReserveData(address)(uint256,uint256,uint256,uint256,uint256,uint256,uint256,uint256,uint256,uint256,uint256,uint40)" 0xda10009cbd5d07dd0cecc66161fc93d7c9000da1 --rpc-url https://rpc.ankr.com/arbitrum命令获得相关数据。
使用totalStableDebt(固定利率债务总价值)与totalDebt(债务总价值)可以计算得到 $ratio$ ,计算结果为0.01399,小于 $O_{ratio}$ 的数值0.2,故而我们不用考虑 $ratio$ 对于利率的影响,可以直接使用以下公式计算:
$$ 0.05 + \frac{0.3941}{0.8000} \times 0.005 = 0.05246 $$
使用上述 $Actual\ APY$ 公式转换得到 实际利率为 $0.05386$,与页面显示一致,如下图:

其实在getReserveData函数的返回值内stableBorrowRate即代表当前资产流动性池的固定利率,此数值除以 $10^{27}$ 即可获得单利条件下的利率,即0.05246,此数值与我们的计算结果一致。同理,variableBorrowRate代表浮动利率,也可以通过除以 $10^{27}$ 的方式转换为单利。
其他模式
isolation mode
我们可以在Assets to supply内发现部分资产的是否能成为贷款抵押资产Can be collateral栏目内填写有Isolation单词,这说明此资产属于Isolation model内的资产。
任何项目都可以将项目代币申请为AAVE交易对的成员,但过去由于所有资产都可以作为质押品贷出资产,这导致AAVE治理委员会要求申请AAVE交易对的代币必须满足一系列严格的要求。这使得AAVE的可交易的资产种类较少。
下图展示了对于一般代币进入AAVE的评级方法:
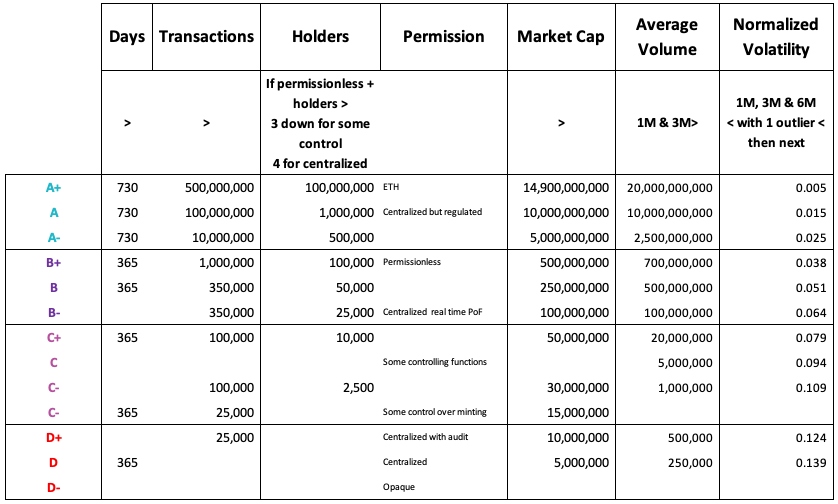
为了解决这些问题,AAVE引入了isolation mode,进入isolation mode的代币位于一个特定的流动性池内,仅能用于贷出稳定币且具有债务上限。这使得部分早期项目的代币也可以进入AAVE的交易池,比如这个。
下图展示了在isolation mode下,我们只能使用$Token2代币贷出稳定币:
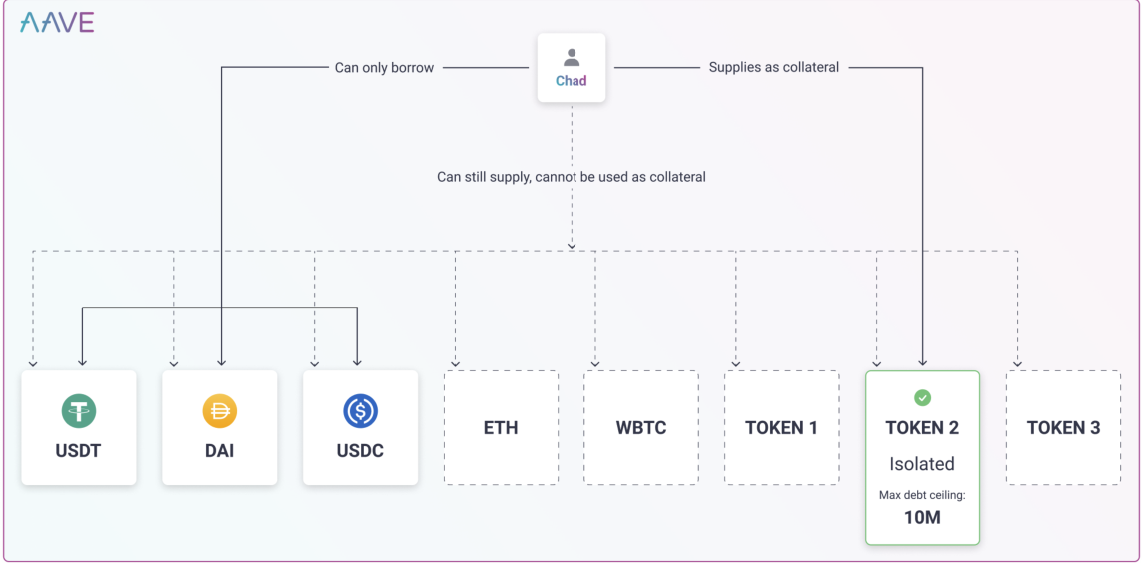
为了更加直观地理解此概念,我们为大家在测试网内展示如何使用isolation mode。我们首先前往Faucet领取EURS代币。在EURS代币内重复上述流程,最终结果如下图:
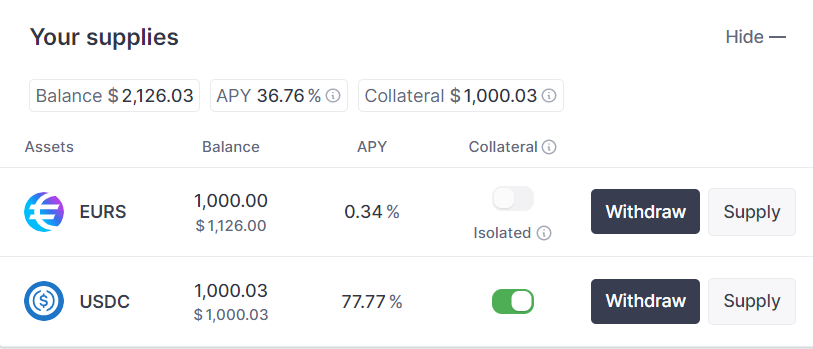
为了进入isolation mode,我们需要首先偿还所有贷出代币,然后关闭USDC的Collateral功能,然后打开EURS的Collateral功能。通过上述操作,我们可以进入isolation mode,最终结果如下:
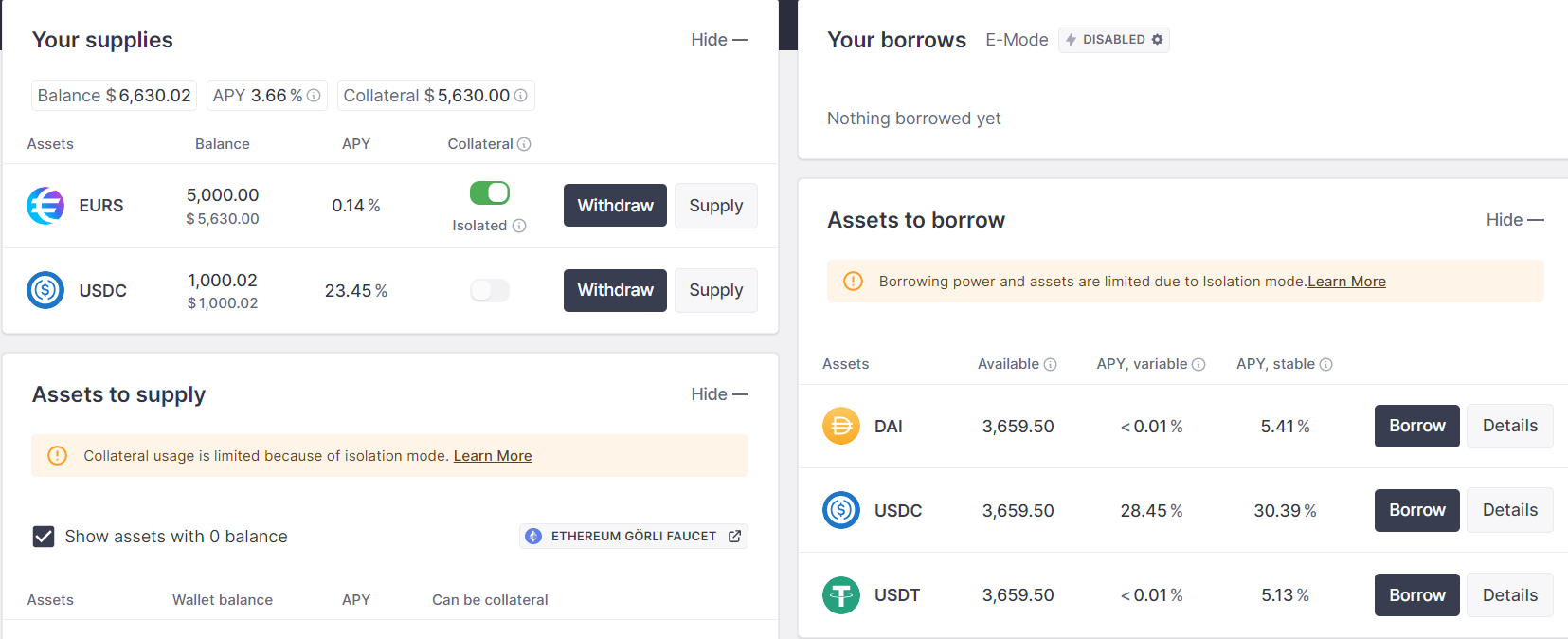
然后,我们可以贷出稳定币资产。退出isolation mode的步骤如下:
- 偿还在
isolation mode中贷出的资产 - 关闭
EURS的Collateral功能
关闭
Collateral功能实质上是关闭了将此代币作为质押品的功能
可能有读者好奇,我可不可以即使用isolation model中的资产和正常资产混用进行贷款等操作? 答案是不可以。可见isolation model具有一定缺陷,具体有以下几种:
- 严重的流动性割裂。当流动性提供商面对大量的
isolation model内的各类资产,基于逐利的本性,流动性提供商会进一步分割其资产以达到利益最大化,这导致部分流动性池内的资产可能较少。 - 降低的用户体验。在正常模式中,用户的抵押品是汇总的,我们无需考虑可以直接使用质押品贷出资产。但对于
isolation,我们需要为每一个分离的资产建立独立的头寸,并进行单独管理,这大大降低了用户的体验。
更加完整的讨论可以参考AAVE V3 Technical Paper
E-Mode
此模式也是AAVE V3引入的,用于带有强相关性资产的抵押和贷款,比如USDT/DAI/USDC稳定币等,这些资产具有本质上的价值一致性,我们认为这些资产之间的抵押和贷款风险都较低。在正常模式下,使用DAI仅能贷出相当于DAI价值80%的其他稳定币,这显然不太合理,当我们启用E-Mode后,DAI可以借出97%价值的稳定币。
一个展示普通模式与E-Mode差别的示意图如下:
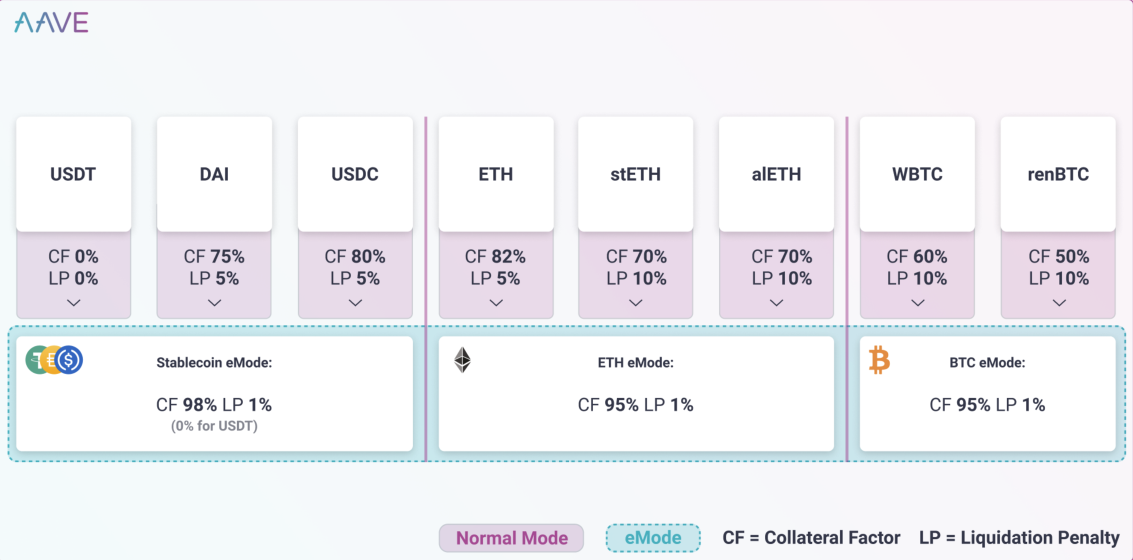
启用此模式时,我们需要点击You Brrows左侧的DISABLED,如下图:
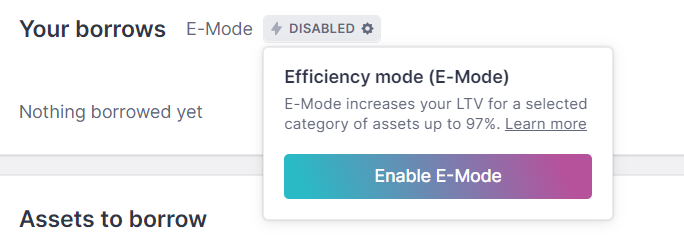
点击后同意交易即可进入E-Mode模式享受对部分资产的超高LTV。推出此模式只需要在此点击You Brrows左侧的按钮即可,但需要注意Health factor,如下图:
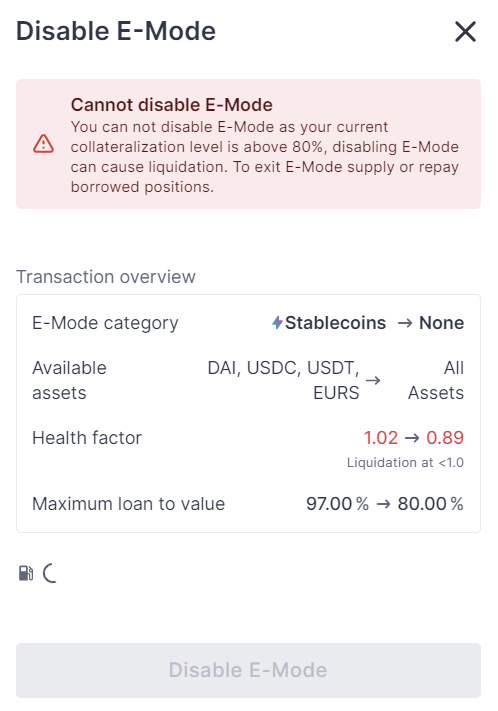
读者可以注意到此处显示Health factor在退出E-Mode时已经小于1,所以此时如果我们一旦退出E-Mode会导致资产被立即清算。读者在退出E-Mode时需要注意此数值,可以在偿还部分贷款后再退出。
总结
本文基本介绍了正常情况下与AAVE交互所需要的基本知识,如下:
- 质押的步骤与质押利率计算
- 贷款步骤与贷款浮动利率、固定利率计算
isolation mode和E-Mode模式的进入和退出
本文没有涉及$AAVE的代币经济学和AAVE安全保险,这部分内容会在下一篇文章介绍。